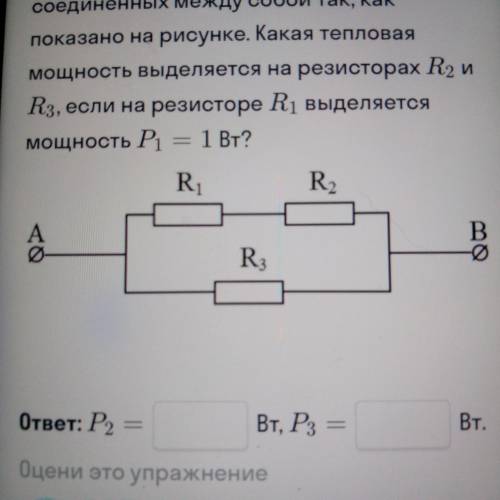
участок AB электрической цепи состоит из трех резисторов с сопротивлениями R¹=10 ом R²= ом,R³ =30 ом, соединенных между собой такой, как показана на рисунке. какая тепловая мощность выделяется натрезисторах R² и R³, если на резисторе R¹ выделяется мощность P¹=1 Ват

Для решения данной задачи мы можем использовать закон Джоуля-Ленца, который устанавливает связь между тепловой мощностью P, проходящим через резистор, и его сопротивлением R, а также силой тока I, протекающего через резистор:

P = I^2 * R

Мы знаем, что на резисторе R¹ выделяется мощность P¹ = 1 Ватт и его сопротивление R¹ = 10 ом. Для решения задачи нам необходимо найти силу тока I, протекающего через этот резистор, так как сила тока будет одинаковой для всех резисторов, соединенных последовательно.

Зная закон Ома, можем выразить силу тока I, протекающего через резистор R¹, следующим образом:

I = U / R,
где U - напряжение, падающее на резисторе R¹.

Поскольку резисторы R² и R³ соединены последовательно, на них также будет падать напряжение U, поэтому сила тока I, протекающего через резистор R¹, будет также равна силе тока, протекающей через резисторы R² и R³.

Теперь найдем напряжение U, падающее на резисторе R¹. Для этого воспользуемся формулой:

P = U * I,
где P - мощность, равная 1 Ватт (выделяющаяся на резисторе R¹), I - сила тока (которую мы ищем), U - напряжение на резисторе R¹.

Таким образом, подставим известные значения в формулу и найдем силу тока I:

1 Ватт = U * I,
1 Ватт = U * (U / R¹),
1 Ватт = U^2 / 10 ом.

Умножим обе части уравнения на 10 ом:

10 ом * 1 Ватт = U^2,
10 ом * 1 Ватт = U^2.

Теперь найдем напряжение U:

У = √(10 ом * 1 Ватт) = √10 ом * √1 Ватт = √10 Вольт.

Таким образом, напряжение на резисторе R¹ равно √10 Вольт.

Мы уже рассмотрели, что сила тока I, протекающая через резисторы R² и R³, будет также равна силе тока, протекающей через резистор R¹.

Теперь мы можем найти тепловую мощность, выделяемую на резисторах R² и R³, используя закон Джоуля-Ленца:

P² = I^2 * R²,
P³ = I^2 * R³.

Подставим значения:

P² = I^2 * R² = (√10 Вольт)^2 * R² = 10 Вольт * R²,
P³ = I^2 * R³ = (√10 Вольт)^2 * R³ = 10 Вольт * R³.

Тогда, мощность выделяемая на резисторе R² равна 10 Вольт * R², а мощность, выделяемая на резисторе R³, равна 10 Вольт * R³.

Обратите внимание, что для расчета тепловой мощности нам необходимо знать значения сопротивлений R² и R³. Если в условии задачи не указано значение R², то невозможно точно определить мощность, выделяемую на резисторе R². То же самое относится и к значению сопротивления R³.