, у меня экзамен! прямоугольная рамка со сторонами а=5 см и b=10 см, состоящая из N=20 витков, помещена во внешнее однородное магнитное поле с индукцией B=0.2 Тл. Нормаль к рамке составляет с направлением магнитного поля угол
Определите вращающий момент сил, действующих на рамку, если по ней течет ток I=2 A.
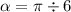
Другие вопросы по теме Физика
Популярные вопросы
- Какое выразительное средство использовал А.С.Пушкин, описывая старую...
3 - Как называется текст оперы, основанный на литературном сюжете?...
2 - Используя карту «Нефтяная промышленность Казахстана»a) Определите,...
3 - Образуй и запиши словасочетания ,используя предлоги ,слова-предметы...
3 - 1)Приведите формулу S-глутамина.Обозначьте его стереохимическую...
2 - 6-сынып ағылшыннан ТЖБ ответь бар ма???...
3 - Ширина прямоугольного параллелепипеда равна 6 см, что составляет...
3 - Өрнектерінің мәндерін салыстырыңдар. 1) 100 000 – 82 109 және 100...
2 - Какой проможуток времени используют для метеонаблюдений в климатологии...
1 - Миссионердің басты мақсаты не...
2
1. Найдем площадь петли. У нас рамка является прямоугольником со сторонами а=5 см и b=10 см. Площадь петли равна A = a * b = 5 см * 10 см = 50 см^2.
2. Подставим известные значения в формулу. У нас N = 20 витков, I = 2 A, A = 50 см^2, B = 0.2 Тл, α = π / 6 рад.
M = 20 * 2 A * 50 см^2 * 0.2 Тл * sin(π / 6) = 2000 см^2АТл * sin(π / 6).
3. Найдем значение sin(π / 6). Этот угол можно представить, как 30 градусов, тогда sin(π / 6) = sin(30°) = 1/2.
M = 2000 см^2АТл * 1/2 = 1000 см^2АТл.
Таким образом, вращающий момент сил, действующих на рамку, равен 1000 см^2АТл.
Обратите внимание, что в данной задаче все значения даны в разных единицах: сантиметры, амперы, теслы. Поэтому мы должны быть осторожны и приводить все данные к одним единицам измерения перед подстановкой их в формулу.