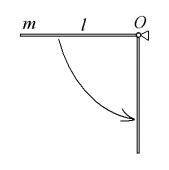
Тонкий однородный стержень массы m и длины l может вращаться в вертикальной плоскости вокруг горизонтальной
оси, проходящей через конец стержня О. Стержень приводят в
горизонтальное положение и отпускают без толчка. Найдите скорость центра масс стержня в момент прохождения им положения равновесия. Сопротивлением воздуха пренебречь. m=5, l=6, g=10.

Для решения этой задачи мы можем использовать закон сохранения механической энергии. Изначально стержень находится в вертикальном положении, поэтому его потенциальная энергия равна 0. В момент прохождения им положения равновесия, потенциальная энергия стержня также будет равна 0.

Потенциальная энергия стержня в горизонтальном положении может быть записана как:

P.E. = mgh,

где m - масса стержня, g - ускорение свободного падения, h - высота стержня над точкой О. В данном случае, h равняется l, так как положение равновесия находится на середине стержня.

Таким образом, потенциальная энергия в горизонтальном положении будет:

P.E. = mgl.

Следовательно, механическая энергия стержня в момент прохождения положения равновесия будет также равна mgl.

Механическая энергия стержня может быть представлена как сумма его потенциальной и кинетической энергии:

E = P.E. + K.E.

Так как потенциальная энергия в момент прохождения положения равновесия равна 0, механическая энергия стержня в этот момент составляет только его кинетическую энергию.

K.E. = mgl.

Также известно, что формула кинетической энергии вращательного движения вокруг оси прохождения через центр масс стержня равна:

K.E. = (1/2)Iω^2,

где I - момент инерции стержня относительно его оси вращения, ω - угловая скорость вращения стержня.

Исходя из геометрии стержня, момент инерции I можно записать как:

I = (1/3)mL^2,

где L равна длине стержня.

Таким образом, формула кинетической энергии вращательного движения стержня примет вид:

K.E. = (1/2)(1/3)mL^2ω^2.

Из закона сохранения механической энергии, мы знаем, что механическая энергия системы должна оставаться постоянной. Таким образом, мы можем записать уравнение:

mgl = (1/2)(1/3)mL^2ω^2.

Отсюда мы можем выразить угловую скорость ω:

ω^2 = (3gl)/(L^2).

Заменив значения констант m, g и L числами из задания, получим:

ω^2 = (3*10*6)/(6^2),

ω^2 = 15.

Теперь мы можем найти скорость центра масс стержня. Скорость центра масс стержня вращается вместе с ним и равна произведению его угловой скорости на расстояние от центра масс стержня до оси вращения. В данном случае, это половина длины стержня, или L/2.

V = ω(L/2).

Заменив значение ω и L из задания, получим:

V = √15(6/2),

V = √45,

V ≈ 6.71.

Таким образом, скорость центра масс стержня в момент прохождения положения равновесия будет около 6.71 единиц скорости.