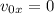1. Физика
  2. Тело скатывается с наклонной

Тело скатывается с наклонной плоскости высотой 4,5 м., имеющей угол наклона 300, за 3 секунды. Определите скорость тела на середине пути.

TadaseXotory TadaseXotory    2   08.07.2020 09:55    3

Ответы
rtgreezz rtgreezz  15.10.2020 15:16

7,35 м/с

Объяснение:

Мы имеем дело с равноускоренным движением вдоль наклонной плоскости. Путь, пройденный телом, совпадает с длинной наклонной плоскости, которую легко можно рассчитать зная высоту наклонной плоскости и её угол наклона:

l=\frac{h}{sin\alpha } =\frac{4.5}{sin30^0}=9 м

Данный путь проходится за 3 секунды, составим же уравнение движения тела и найдем из него ускорение (ось х направим вдоль наклонной плоскости вниз):

x(t)=x_0+v_0_xt+\frac{a_xt^2}{2}=\frac{a_xt^2}{2}

Ускорение:

a_x=\frac{2x(t)}{t^2}

С учетом того, что при t=3 c, x(3)=9 м

a_x=\frac{2*9}{3} =6 м/с²

Для нахождения скорости в середине наклонной плоскости (то есть по прохождению расстояния в 4,5 м) можно воспользоваться коротким путем, а именно задействовать формулу "путь без времени":

s=\frac{v_x^2-v_0_x^2}{2a_x}

Теперь просто выразим отсюда скорость, при этом учтем, что s=4.5 м (середина пути), а начальная скорость v_0_x=0

v_x=\sqrt{2a_xS} =\sqrt{2*6*4.5}=7.35 м/с.


Тело скатывается с наклонной плоскости высотой 4,5 м., имеющей угол наклона 300, за 3 секунды. Опред
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
nastosetrova1 nastosetrova1  12.08.2019 02:30
Вкотле паровой машины температура равна 160°с, а температура холодильника 10°с. какую максимальную работу можно теоретически получить от машины, если в топке, коэффициент...
ezdar04 ezdar04  12.08.2019 02:30
Шарик массой 10 кг свободно падает с высоты 2 м и отражается от установленного на неподвижной тележке щита, плоскость которого наклонена к горизонту под углом 450. с...
2006anna1 2006anna1  12.08.2019 02:30
Какая энергия выделится при отвердевании 2,5 кг серебра, взятого при температуре плавления, и его дальнейшем охлаждении до 160 °с?...
hgfdui hgfdui  21.04.2020 17:43
Насос щогодини подає на висоту 36 м воду об’ємом 2,2 м3 . Сила струму в електродвигуні насоса, підключеного до мережі постійного струму з напругою 110 В, дорівнює 4 А....
nastyagosteva nastyagosteva  11.09.2019 06:00
Насколько удлинится канат жесткость которого 1800 н/м под действием 10,8н?...
mirza22 mirza22  11.09.2019 06:00
Два основных последствий действий силы на тело...
frausadykova20 frausadykova20  25.06.2019 06:50
12 горошин положили в ряд.длина ряда -7,2 см.найти диаметр горошины....
natashakuznecz1 natashakuznecz1  25.06.2019 06:50
1.чем кроме температуры горячее тело отличается от холодного? 2.в какие виды энергии превращается кинетическая энергия метеорита после его сгорания в атмосфере?...
perf3ctkn1ghtozbgjn perf3ctkn1ghtozbgjn  25.06.2019 06:50
Автомобиль массой 900кг движется равномерно по прямолинейному участку шоссе. его двигатель развивает силу тяги 550н. изобразите инайдите все силы действующие на автомобиль....
Ямайкамафака Ямайкамафака  25.06.2019 06:50
Яку роботу виконав учень переміщуючи деревяний брусок по деревяній лінійці на відстань 0.8. маса бруска 85 г...

Популярные вопросы