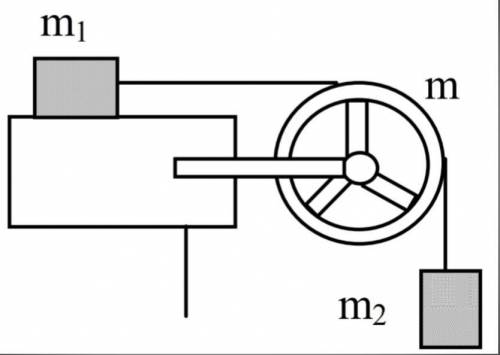
Тело массой m1 = 0,26 кг (рис.), соединенное
невесомой нитью посредством блока (в виде
полого тонкостенного цилиндра) с телом массой
m2 = 0,2 кг, скользит по поверхности
горизонтального стола. Масса блока m = 0,15 кг.
Коэффициент трения f тела о поверхность равен
0,2. Пренебрегая трением в подшипниках,
определить: 1) ускорение а, с которым будут двигаться эти тела; 2) силы
натяжения Т1 и Т2 нити по обе стороны блока.

Добрый день! Давайте разберем эту задачу по шагам.

1) Найдем суммарную силу, действующую на систему тел. Разделим эту силу на суммарную массу тел, чтобы найти ускорение:
F_сум = m * a

На систему действуют следующие силы:
- Сила тяжести для тела массой m1: F_тяж = m1 * g
- Сила трения, действующая на тело массой m1, равна: F_тр1 = μ * N, где μ - коэффициент трения, N - нормальная реакция.
- Сила трения, действующая на блок массой m, равна: F_тр2 = μ * N
- Сила натяжения нити с одной стороны блока: F_Т1
- Сила натяжения нити с другой стороны блока: F_Т2

2) Найдем нормальную реакцию N. Для этого возьмем систему тел м1, m и блок и рассмотрим равновесие по вертикальной оси:

N + F_тяж - F_тяж2 = 0

где F_тяж2 - сила тяжести для блока. Так как блок невесомый, F_тяж2 = 0, значит:

N + F_тяж = 0

N = -F_тяж

3) Подставим значение нормальной реакции N в выражения для сил трения:
F_тр1 = μ * (-F_тяж)
F_тр2 = μ * (-F_тяж)

4) Найдем силы натяжения нити F_Т1 и F_Т2. Для этого рассмотрим равновесие блока по горизонтальной оси:

F_Т1 + F_Т2 + F_тр2 + F_тр1 = 0

Подставим значения сил трения и нормальной реакции:

F_Т1 + F_Т2 + μ * (-F_тяж) + μ * (-F_тяж) = 0

F_Т1 + F_Т2 - 2μ * F_тяж = 0

5) Найдем силу трения F_тр1. Для этого воспользуемся формулой:

F_тр1 = μ * N = μ * (-F_тяж)

6) Подставим найденные значения в уравнение равновесия блока и решим его относительно сил натяжения нити:
F_Т1 + F_Т2 - 2μ * F_тяж = 0

F_Т1 + F_Т2 = 2μ * F_тяж

F_Т1 + F_Т2 = 2μ * m1 * g (так как F_тяж = m1 * g)

7) Подставим это равенство в уравнение, найденное на шаге 4 и решим его относительно сил натяжения нити:
2μ * m1 * g - 2μ * F_тяж = 0

2μ * m1 * g = 2μ * F_тяж

F_Т1 + F_Т2 = F_тяж

F_Т1 + F_Т2 = m1 * g

Теперь можно перейти к решению задачи численным методом. Для этого подставим известные значения в полученные выражения.

m1 = 0,26 кг
m2 = 0,2 кг
m = 0,15 кг
μ = 0,2
g = 9,8 м/с²

Сначала найдем силу тяжести для тела массой m1:
F_тяж = m1 * g = 0,26 * 9,8 = 2,548 Н

Затем найдем нормальную реакцию:
N = -F_тяж = -2,548 Н

Далее найдем силы трения:
F_тр1 = μ * (-F_тяж) = 0,2 * (-2,548) = -0,5096 Н
F_тр2 = μ * (-F_тяж) = 0,2 * (-2,548) = -0,5096 Н

Суммируем силы трения:
F_тр = F_тр1 + F_тр2 = -0,5096 - 0,5096 = -1,0192 Н

Теперь найдем ускорение системы тел:
F_сум = m * a
F_сум = m1 * g - F_тр
2,548 = (0,26 + 0,2 + 0,15) * a - 1,0192
2,548 = 0,61 * a - 1,0192
2,548 + 1,0192 = 0,61 * a
3,5672 = 0,61 * a
a ≈ 5,85 м/с²

Наконец, найдем силы натяжения нити:
F_Т1 + F_Т2 = m1 * g
F_Т1 + F_Т2 = 0,26 * 9,8
F_Т1 + F_Т2 ≈ 2,548 Н

Получается, что сумма сил натяжения нити равна 2,548 Н. Распределение этих сил натяжения по обе стороны блока будет зависеть от коэффициента трения μ и массы блока m.

Это и является полным решением задачи. Если у вас есть еще вопросы, с удовольствием помогу!