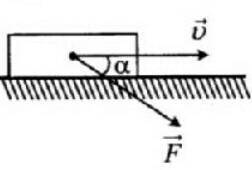
Тело массой 1 кг движется по горизонтальной плоскости. На тело действует сила F под углом a=30° к горизонту (см. рисунок). Коэффициент трения между телом и плоскостью равен 0,4. Каков модуль силы F, если модуль силы трения, действующий на тело, равен 6Н?​

Добрый день, рассмотрим ваш вопрос. Для решения этой задачи нам понадобятся некоторые основные физические законы и формулы.

Сначала рассмотрим силы, действующие на тело. По условию на тело действуют две силы: сила F под углом 30° к горизонту и сила трения. Мы не знаем модуль силы F, но мы знаем модуль силы трения, который составляет 6 Н.

Силу трения можно вычислить с помощью формулы:

Fтр = μ * N,

где Fтр - модуль силы трения, μ - коэффициент трения, N - нормальная сила (сила, действующая перпендикулярно поверхности).

Так как тело движется по горизонтальной плоскости, то нормальная сила равна силе тяжести, которую можно вычислить по формуле:

N = m * g,

где m - масса тела, g - ускорение свободного падения (приближенное значение 9,8 м/с²).

Теперь, когда у нас есть формула для силы трения и нормальной силы, мы можем решить задачу:

Fтр = μ * N,

Fтр = μ * m * g,

6 = 0,4 * 1 * 9,8,

6 = 3,92.

Таким образом, модуль силы трения равен 3,92 Н.

Далее, сила F разлагается на горизонтальную и вертикальную составляющие. Горизонтальную составляющую силы F можно найти с помощью следующей формулы:

Fх = F * cos(a),

где Fх - горизонтальная составляющая силы F, a - угол между силой F и горизонтом.

В нашем случае:

Fх = F * cos(30°).

У нас есть только модуль силы трения, поэтому мы не знаем точного значения силы F, чтобы найти его модуль. Однако, мы можем найти отношение горизонтальной составляющей силы F к силе трения:

Fх / Fтр = cos(30°).

Теперь мы можем найти модуль силы F:

F = Fх / (cos(30°)).

Подставив известные значения:

F = (Fх / (cos(30°)),

F = (6 / (cos(30°)).

Подставим численное значение угла:

F = 6 / (0,866).

Таким образом, модуль силы F равен примерно 6,93 Н.

В итоге, модуль силы F, действующей под углом 30° к горизонту, равен примерно 6,93 Н.