Тело брошено вертикально вверх с высоты 5 м со скоростью 20 м/с. На какой
высоте его скорость станет 10 м/с?
РЕШИТЬ ПО ФОРМУЛАМ ЗАКОНА СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ.
ЗА КОПИРОВАНИЕ ДРУГИХ ОТВЕТОВ ЖАЛОБА
Другие вопросы по теме Физика
Популярные вопросы
- Первую половину пути велосипедист проехал со скоростью 36 км/ч, затем...
3 - Запишите уравнение диссоциации веществ формулы которых : а)hbr б)koh...
1 - Напишите краткий анализ «бедная лиза» карамзина. примерно на 1 лист....
1 - 15 характер и поведение мити из романа дубровский...
3 - 30 і скласти діалог дискусійного характеру на тему після перегляду телепередач...
1 - Характер героя в рассказе тонино невидимка,...
1 - Всем ! решить по языку ребенку не могу ,сама учила ,...
1 - Что для тебя значит быть терпимым по отношению к людям, живушим с вич/спид...
2 - Самолет, скорость которого 840 км/ч, пролетел за 3 часа расстояние,...
3 - Валя шифрует слова (последовательности букв), записывая вместо каждой...
2
20м
Объяснение:
в начальный момент времени = 20м/с,
= 20м/с, 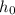 = 5м
= 5м
когда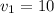 м/с
м/с
но энергия неизменна, то есть