1. Физика
  2. Свинцовая пуля, которая двигалась

Свинцовая пуля, которая двигалась со скоростью 300 м/с , ударилась о металлическую пластину и остановилась. какая часть свинца расплавилась, если считать, что свинец полностью поглотил энергию, которая выделилась при ударе? начальная температура шара 27 ∘ с . (нужен приблизительный ответ)

ната12354 ната12354    1   02.10.2019 10:30    4

Ответы
nparshina14 nparshina14  09.10.2020 11:33
Дано:

Скорость пули: V = 300 м/с.

Начальная температура свинца: t₁ = 27 °C.

Температура плавления свинца: t₂ = 327 °C.

Удельная теплоёмкость свинца: с = 140 Дж/(кг * °С).

Удельная теплота плавления свинца: λ = 25000 Дж/кг.

Обозначим массу всей пули через m₁, а массу расплавленной части пули через m₂.

Найти отношение масс: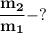 \bf\dfrac{m_2}{m_1} - ?

Решение:

0. Кинетическая энергия летящей пули переходит в теплоту нагревания свинца и его плавления, то есть: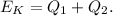 E_K = Q_1 + Q_2.

1. Кинетическая энергия летящей пули: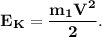 \bf E_K = \dfrac{m_1V^2}{2}.

2. Энергия (теплота) нагревания пули: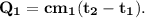 \bf Q_1 = cm_1(t_2 - t_1).

3. Теплота плавления части пули: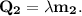 \bf Q_2 = \lambda m_2.

4. Объединяем (0), (1), (2) и (3):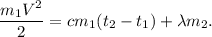 \dfrac{m_1V^2}{2} = cm_1(t_2 - t_1) + \lambda m_2.

5. Выразим искомое отношение из (4).

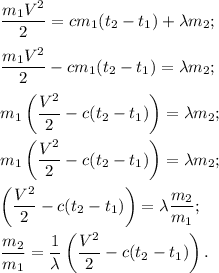
\dfrac{m_1V^2}{2} = cm_1(t_2 - t_1) + \lambda m_2;\\\\\dfrac{m_1V^2}{2} - cm_1(t_2 - t_1) = \lambda m_2;\\\\m_1\left(\dfrac{V^2}{2} - c(t_2 - t_1)\right) = \lambda m_2;\\\\m_1\left(\dfrac{V^2}{2} - c(t_2 - t_1)\right) = \lambda m_2;\\\\\left(\dfrac{V^2}{2} - c(t_2 - t_1)\right) = \lambda \dfrac{m_2}{m_1};\\\\\dfrac{m_2}{m_1} = \dfrac{1}{\lambda}\left(\dfrac{V^2}{2} - c(t_2 - t_1)\right).

Численно получим: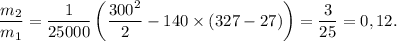

\dfrac{m_2}{m_1} = \dfrac{1}{25000}\left(\dfrac{300^2}{2} - 140\times (327 - 27)\right) = \dfrac{3}{25} = 0,12.

ответ: 0,12 часть.
ПОКАЗАТЬ ОТВЕТЫ
kirill12123 kirill12123  09.10.2020 11:33

Решение на фото. Расплавилась только 1/8 всей пули.


Свинцовая пуля, которая двигалась со скоростью 300 м/с , ударилась о металлическую пластину и остано
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Uuuuuu2006 Uuuuuu2006  30.10.2020 12:07
ТЕКСТ ЗАДАНИЯ Может ли путь быть меньше расстояния между начальной и конечной точками траектории?ответы:да, так как длина траектории может быть меньше перемещенияВпереднет,...
школоллло школоллло  30.10.2020 12:07
знайдіть масу сонця уважаючи що відстань між сонцем і землею=1,5×10`11м.земля рухається навколо сонця зі швидкістю 310`4м/с​...
Cat6661313 Cat6661313  30.10.2020 12:07
А где Каковы координаты поезда к моменту его остановки? Определите длину перемещения и путь, пройденный поездом за все время движения....
IgorGr1ef IgorGr1ef  30.10.2020 12:07
Потяг якої маси може рухатися з прискоренням 0,1 м/с2 при коефіцієнті тертя 0,005, якщо він розвиває максимальне тягове зусилля 300 кН? І МОЖНО З МАЛЮНКОМ БУДЬ-ЛАСКА...
nadezhdalipchan nadezhdalipchan  30.10.2020 12:07
Текст ЗАДАНИЯ Выберите рисунок, на котором изображено прямолинейное равномерное движение. Следует учесть, чтовсе промежутки времени одинаковые,Выберите 1 ответ-1)2)1)1)...
saule844007 saule844007  30.05.2019 21:20
1.период колебаний маятника 0.8с. определите число колебаний за 16с. 2.чему равна частота колебаний тела, совершившего за 2 мин 60 колебаний? 3.чему равен период колебаний...
demianchik demianchik  30.05.2019 21:20
Почему можно сплошные брусья, подвергающиеся изгибу, заменять трубами, не уменьшая прочности?...
pavdora073539 pavdora073539  30.05.2019 21:20
Почему к наэлектризованной расчёске будет притягиваться струйка воды ? объясните свой ответ....
tinkimolko tinkimolko  30.05.2019 21:20
Шарик массой 0.2 кг закрепленный на пружине жесткостью 200н/м. амплитуда колебаний шарика равна 4 см. с какой скоростью шарик проходит положение равновесия?...
darik2042005p07x0l darik2042005p07x0l  30.04.2020 12:47
Під час електролізу поверхню сталевої деталі площею 800 см2покрито шаром нікелю завтовшки 54 мкм. За якої сили струму проходив процес, якщо електроліз тривав 4 години?​...

Популярные вопросы