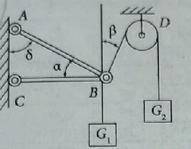
Стержни АВ и ВС соединены между собой и вертикальной стеной шарнирно. К шарниру В подвешены два груза: G1 - подвешен вертикально, G2 - через блок D. Пренебрегая силами трения и размерами блока D, определить усилия в стержнях АB и СВ. Данные: G1=22 kH, G2=4 kH, a= 25°, B=70°, б=20°

Добрый день! Давай разберемся с этой задачей. Для начала, нам нужно определить направление и силы в стержнях AB и BC с помощью его условий и изображения. Из условия задачи известно, что стержни АВ и ВС соединены между собой и вертикальной стеной шарнирно. К шарниру В подвешены два груза: G1 - подвешен вертикально, G2 - через блок D. Также нам даны значения углов: alpha (α) равен 25 градусам, beta (β) равен 70 градусам и gamma (γ) равен 20 градусам. Давай начнем с определения направления сил в стержнях. Мы можем предположить направление силы в стержне AB, отклонив его от вертикали под углом α вниз. Для стержня BC, мы можем предположить направление силы, отклонив его от вертикали под углом γ вправо. Теперь, обратимся к силам, действующим на шарнир В. На шарнир В действуют две силы: сила G1, направленная вертикально вниз, и сила G2, проходящая через блок D. Начнем с силы G1. Эта сила действует вертикально вниз и она равна 22 кН. Теперь обратимся к силе G2. У нас есть сведения о грузе G2 и блоке D, который связан с шарниром В. Здесь нам нужно помнить, что блок D не имеет размеров и силы трения для нас не существуют. Это означает, что сила G2, которая проходит через блок D, будет направлена в сторону стерженя BC. Поскольку угол В равен 70 градусам, мы можем разделить силу G2 на 2 компонента: одну, направленную вниз (component G2_y) и одну, направленную вправо (component G2_x) на стержень BC. Чтобы найти эти компоненты, мы можем использовать тригонометрию. component G2_y = G2 * sin(B) component G2_y = 4 кН * sin(70°) component G2_y ≈ 3.61 кН component G2_x = G2 * cos(B) component G2_x = 4 кН * cos(70°) component G2_x ≈ 1.26 кН У нас есть все необходимые силы и компоненты, чтобы решить эту задачу. Выразим каждую из сил в стержнях AB и BC через силы и компоненты, которые мы определили ранее. Затем мы можем использовать уравновешенность силы в горизонтальной и вертикальной плоскостях, чтобы найти усилия в стержнях AB и BC. Суммируем все вертикальные силы: Σ F_vertical = G1 - component G2_y = 22 кН - 3.61 кН Теперь суммируем все горизонтальные силы: Σ F_horizontal = - component G2_x Теперь, преобразуем наши уравнения суммы силы в горизонтальной и вертикальной плоскостях к Σ F_vertical = 0 и Σ F_horizontal = 0: Σ F_vertical = 22 кН - 3.61 кН = 0 Σ F_horizontal = -1.26 кН = 0 Из уравнения Σ F_vertical = 0 мы можем выразить силу в стержне AB: F_AB = 3.61 кН - 22 кН F_AB = -18.39 кН (так как сила направлена вверх, мы можем использовать отрицательное значение) Из уравнения Σ F_horizontal = 0 мы можем выразить силу в стержне BC: F_BC = -1.26 кН Итак, усилие в стержне AB равно -18.39 кН, а усилие в стержне BC равно -1.26 кН. Надеюсь, что мое объяснение помогло вам понять решение этой задачи. Если у вас возникнут еще вопросы, не стесняйтесь задавать.