Стеоремы остроградского-гаусса вывести формулу для расчёта напряжённости поля металлического шара, заряженного зарядом q. построить график

Закон Гаусса:

Поток напряженности электрического поля через произвольную поверхность, окружающую тело, равен заряду тела, умноженному на 4π.

Окружим заряженный шар сферой,  радиуса r.

Сначала положим r>R, где R - радиус шара.

Из вышеописанного закона:

, где интеграл берется по поверхности радиуса r.

Из симметричности задачи следует, что напряженность E в каждой точке сферы r одинакова (и направлена вдоль радиуса), то есть E=const в подинтегральм выражении. Тогда:

.

Отсюда: .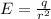

Для нахождения поля внутри шара, при r<R, введем объемную плотность заряда:

.

Аналогично, найдем поток напряженности поля через сферу, радиуса r. Точно также, из симметрии, считаем E = const (на этой сфере). Тогда:

.

Здесь, q_{in} - заряд шара, радиуса r:

.

Подставляя в выражение для E, получим:

.

Ниже представлен график модули напряженности электрического поля для всех r.