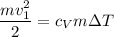Сосуд, содержащий некоторую массу азота при н.у. ( температура нулевая = 0 градусов цельсия, давление нулевое = 10^5 па), движется со скоростью 100 м/с. удельная теплоемкость азота при постоянном объеме равна 745 дж/кг*к. при внезапной остановке сосуда максимальная температура азота будет равна?
Другие вопросы по теме Физика
Популярные вопросы
- Как записать в два столбика: однокоренные слова и формы одного слова?...
3 - Вхимчистку отдали 12 платьев брюк на 4 больше чем платьев а юбок столько...
2 - Вмолекуле днк количество нуклеотидов с гуанином составляет 5% от бошего...
1 - Чому це бринить у повітрі довгий звук срібних дзвіночків? підкреслити...
3 - Соедините: 1. маллингар 2. вулверхэмптон 3. холмс-чапел 4. донкастер...
2 - Нужно доклад на тему солнце 6 класс! по естествознанию задали!...
1 - Вмешке 60 кг сахаров весь сахар рассыпали в пакеты по 500 г сколько...
3 - Один знаменитый певец написал своему записку.тот отправился в магазин,но...
3 - Решить! в равнобедренный прямоугольный треугольник, каждый катет которого...
2 - Назовите произведение и главного героя, с которым постепенно старел...
2
ответ: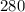 К
К
Объяснение:
Дано:
---------------------------------------------------
Вариант решения №1 - без использования удельной теплоёмкости газа (более сложный)
Согласно ЗСЭ
Отсюда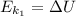
Вариант решения №2 - без учёта того что газ находиться при н.у. (более сложный)
Тут также справедливо равенство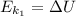
Но тут можно исходить из того что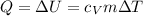
Тогда