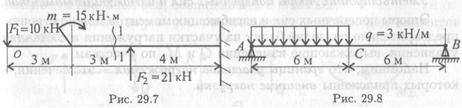
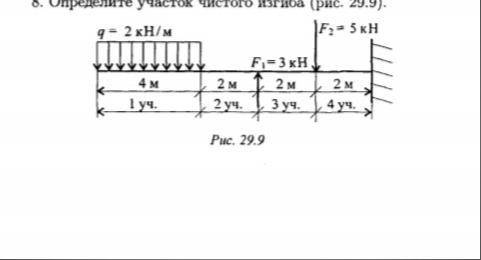
Сопромат 5) Определите поперечную силу и изгибающий момент в сечении 1-1 рис 29.7 6) Определить реакцию в опоре B 7) Определите величину поперечной силы и изгибающего момента в сечении С, использовав схему балки рис 29.8 8)определите участок чистого изгиба рис 29.9

Добрый день! Давайте разберем ваш вопрос шаг за шагом.

1) Определение поперечной силы и изгибающего момента в сечении 1-1, изображенном на рисунке 29.7.

Для начала, давайте рассмотрим данное сечение. На рисунке видно, что есть две силы, действующие на балку - это сила P и сила Q.

Поперечная сила в сечении 1-1 определяется как сумма всех сил, направленных перпендикулярно выбранному сечению. В данном случае, поперечная сила равна сумме силы P и силы Q:

F = P + Q.

Изгибающий момент в сечении 1-1 определяется как произведение поперечной силы на расстояние от выбранного сечения до точки приложения силы. В данном случае, изгибающий момент равен сумме произведений:

M = (P * a) + (Q * b),

где а и b - расстояния от выбранного сечения до точек приложения сил P и Q соответственно.

2) Определение реакции в опоре B.

Для определения реакции в опоре B нужно использовать уравновешивающие моменты. Так как балка находится в равновесии, то сумма моментов равна нулю:

M1 + M2 - Rb * L = 0,

где M1 и M2 - моменты сил P и Q относительно опоры B, L - расстояние между опорами A и B, Rb - реакция в опоре B.

3) Определение величины поперечной силы и изгибающего момента в сечении C, используя схему балки на рисунке 29.8.

На рисунке видно, что в сечении C действуют три силы - P, Q и R.

Поперечная сила в сечении C определяется как сумма всех сил, направленных перпендикулярно выбранному сечению. В данном случае, поперечная сила равна сумме сил P, Q и R:

F = P + Q + R.

Изгибающий момент в сечении C определяется как произведение поперечной силы на расстояние от выбранного сечения до точки приложения силы. В данном случае, изгибающий момент равен сумме произведений:

M = (P * a) + (Q * b) + (R * c),

где a, b и c - расстояния от выбранного сечения до точек приложения сил P, Q и R соответственно.

4) Определение участка чистого изгиба на рисунке 29.9.

На рисунке 29.9 показана балка с различными участками. Участок чистого изгиба - это такой участок балки, где действуют только изгибающие моменты и нет поперечных сил. На рисунке 29.9 таким участком является прямоугольная область с обозначением "чистый изгиб".

В данном случае, для определения участка чистого изгиба нужно учесть все силы и моменты, действующие на балку и проанализировать, где из них только моменты изгиба перевешивают над поперечными силами. Такой участок можно выбрать, например, в середине балки, где поперечная сила равна нулю и остаются только изгибающие моменты.

Надеюсь, этот ответ был понятен для вас. Если у вас возникнут еще вопросы, не стесняйтесь задавать. Я готов помочь вам в изучении сопромата!