с физикой Решите хотя бы одну задачу

Шарик масса m с зарядом q подвешен на тонкой изолирующей нити к вертикальной плоскости, по которой равномерно распределен заряд с поверхностной плотностью σ . Нить образуют с вертикалью угол a, сила натяжения нити равна Fн. Определить массу m, если q = 1650 СГСЭ; σ = 0,4мкКл/м^2; а=35 градусов.

Точечные заряды q1, q2, q3 и q4 находятся в последовательных вершинах квадрата со стороной a. В центре квадрата напряженность электрического поля равна Е, а потенциал . Определить напряженность Е, если q1=+0,15мкКл; q2=+0,27мкКл; q3=+0,32мкКл; q4=- 0,14мкКл; =+12кВ.

Ион с зарядом q=Ze (e - элементарный заряд) и массой M=Am (m - масса протона) ускоряется разностью потенциалов U и влетает в однородное магнитное поле напряженностью H перпендикулярно его силовым линиям. Траектория иона имеет радиус R, время одного оборота Т. Определить радиус R, если Z=6; A=12; U=6,7кВ; H=9,2кА/м.

Ответы

Вазген228 15.10.2020 15:07

1) 1,78 г

2) 19726 В/м

3) 1,44 м

Объяснение:

Задача 1. Сделаем рисунок с указанием всех сил.

Условие равновесия системы имеет вид

F_k+T+mg=0

В проекциях на координатные оси

$\left \{ {{-F_k+Tsin\alpha =0} \atop {-mg+Tcos\alpha =0}} \right.$

Выразим силу натяжения нити Т через кулоновскую силу отталкивания и найдем массу шарика

$T=\frac{F_k}{sin\alpha }$

$m=\frac{F_kctg\alpha }{g}$

Кулоновскую силу можно найти как произведение величины заряда на поле бесконечной заряженной плоскости, коей является стена

$F_k=qE=\frac{q\sigma }{2\epsilon _0}$

Окончательно (конечно переведя заряд в СИ)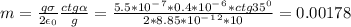 $m=\frac{q\sigma }{2\epsilon _0}\frac{ctg\alpha }{g} =\frac{5.5*10^-^7*0.4*10^-^6*ctg35^0}{2*8.85*10^-^1^2*10} =0.00178$ кг или 1,78 г.

Задача 2.

Найдем сначала расстояние от вершин до центра квадрата, для этого распишем потенциал поля как сумму потенциалов отдельных зарядов

$\phi = \frac{k}{d} (q_1+q_2+q_3+q_4)$

Откуда

$d=\frac{k}{\phi } (q_1+q_2+q_3+q_4)=\frac{9*10^9}{12000}(0.15*10^-^6+0.27*10^-^6+0.32*10^-^6-0.14*10^-^6)=0.45$ м

Согласно принципу суперпозиции, напряженности полей, даваемые противоположными зарядами

$E_1_3=E_1-E_3=\frac{k}{d^2}(q_1-q_3)=\frac{9*10^9}{0.45^2}(0.15*10^-^6-0.32*10^-^6)=-7556$ В/м

$E_2_4=\frac{k}{d^2}(q_2-q_4)=\frac{9*10^9}{0.45^2}(0.27*10^-^6+0.14*10^-^6)=18222$ В/м

Так как угол между ними прямой, для нахождения результирующего заряда воспользуемся теоремой Пифагора

$E=\sqrt{E_1_3^2+E_2_4^2}=\sqrt{7556^2+18222^2}=19726$ В/м.

Задача 3.

Найдем скорость иона перед влетом в поле

$\frac{mv^2}{2}=qU$

$v=\sqrt{\frac{2qU}{m} }=\sqrt{\frac{2*6*1.6*10^-^1^9*6700}{12*1.67*10^-^2^7} }=801197$ м/с

Найдем индукцию поля

$B=\mu _0H=4\pi *10^-^7*9200=0.0116$ Тл

Сила Лоренца сообщает иону центростремительное ускорение, из этих соображений найдем радиус траектории

$qvB=m\frac{v^2}{R}$

$R=\frac{mv}{qB}=\frac{12*1.67*10^-^2^7*801197}{6*1.6*10^-^1^9*0.0116} =1.44$ м.

с физикой Решите хотя бы одну задачу Шарик масса m с зарядом q подвешен на тонкой изолирующей нити к

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Физика

racinskaulana 15.04.2020 16:12

Наклон плоскости характеризует угол α. Даны три наклонные плоскости с различными углами: у 1-й плоскости α1=38 градуса(-ов), у 2-й плоскости α2=54 градуса(-ов), у 3-й плоскости...

sergei66284 15.04.2020 16:12

Чтобы облегчить перемещение груза, Олег использовал наклонную плоскость, высота которой h=0,4 м и длина l=2 м. Какую силу приложил Олег, чтобы переместить груз, если вес груза...

pashnina379 15.04.2020 16:11

Вырази в миллиджоулях. 5,4⋅10−4Дж=0,00054Дж...

FIREH4IR 15.04.2020 16:11

Электроемкость плоского конденсатора 1200 п Ф. Между пластинами конденсатора помещен диэлектрик- слюда (ε=6). Площадь пластин конденсатора 10 см2. Чему равна толщина диэлектрика....

QbQbQb 15.04.2020 16:11

Яблуко масою 300 г висить на гілці на висоті 2 м яку роботу воно може виконати під час падіння...

Сmetana34 15.04.2020 16:11

Фотон рентгенівського випромінювання має енергію 50 кеВ. Яким буде значення енергії фотона в фДж?...

нарешатор 15.04.2020 16:11

Пункты б,в,г,д,ж и можете расписать.Если что я могу написать ответ,но не знаю как расписать....

brilovainna 15.04.2020 16:11

На рисунке изображён прямой проводник...

Vikaadamm 15.04.2020 16:10

Під дією сили 20H тіло перемістилось на 25см.Яка робота виконана при цьому?...

alalosh 15.04.2020 16:10

Як виникають дірки в чистих напівпровідниках?Чому дірку можна розглядати як частинку з позитивним зарядом?...

Популярные вопросы