с 5 моль идеального газа был пооведен процесс, график которого показан на рискнке 75. Какую работу совершил газ в этом процессе, если известно, что в состоянии "2" его температура равна 500К?
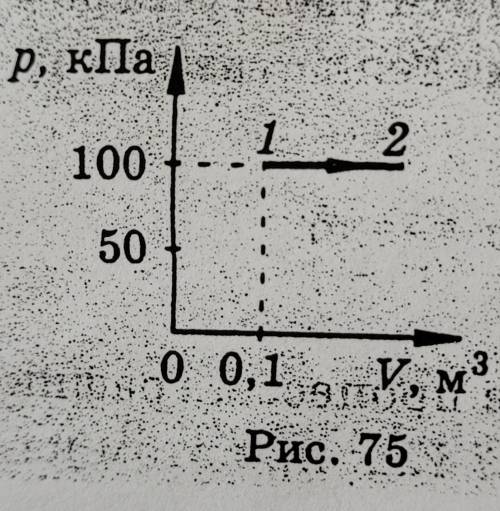
Другие вопросы по теме Физика
Популярные вопросы
- 16)охарактеризуйте отношение католических государств Европы и...
3 - БЫСТРЕЕ Кто первый тому лучший ответ1. Обзор функций главного...
2 - MgSO3^+ + 2H^+ → Mg2^+ + SO2+H2O скороченим йонним рівнянням...
3 - Своими словами объясните правило. Правило : не повреждайте кору...
3 - Туристы взяли в поход 80 л воды в 40 одинаковых бутылках. В первый...
2 - Спроби створити абсолютно ізольовану від біосфери штучну екосистему...
2 - Запишите формулы и Постройте график линейной функции если известно...
3 - 2.Одновалентные очень активные металлы, образующие в реакции с...
3 - У трикутнику ВСD кут D дорівнює 90 градусів, BD=5, CD=6. Чи перпендикулярні...
1 - За 0,1 ч лодка проплыла 3,5 км. Чему равна скорость лодки?...
2
\[ W = \int_{V_1}^{V_2} P(V) dV \]
График на рисунке 75 представляет собой кривую, которая не является простым линейным или параболическим участком. Чтобы определить работу газа, нам необходимо разбить этот процесс на более простые участки и, затем, интегрировать работу газа на каждом из этих участков.
Уравнение для идеального газа можно записать как \[ PV = nRT \], где
\( P \) - давление газа,
\( V \) - объём газа,
\( n \) - количество вещества (в молях),
\( R \) - газовая постоянная,
\( T \) - температура газа.
Мы знаем, что у нас есть 5 молей идеального газа и его температура состоянии "2" равна 500K.
Чтобы посчитать работу газа на каждом участке кривой, необходимо использовать уравнение состояния \( PV = nRT \), чтобы найти давление \( P \) в каждом состоянии. Затем, используя найденное давление, можно интегрировать уравнение работы газа \[ W = \int_{V_1}^{V_2} P(V) dV \] для каждого участка кривой.
Для первого участка кривой, от состояния "1" до состояния "2", процесс осуществляется при постоянной температуре 500K. Это означает, что у нас должна быть прямая линия, так как из уравнения состояния \( PV = nRT \) следует, что при постоянной температуре давление и объем взаимосвязаны линейно.
Давление в состоянии "2" можно найти, зная, что у нас 5 молей газа и его температура равна 500K:
\[ P_2V_2 = nRT \]
\[ P_2V_2 = (5 \, \text{моль})(8,31 \, \text{Дж/моль} \cdot \text{К})(500 \, \text{К}) \]
\[ P_2V_2 = 20775 \, \text{Дж} \]
Таким образом, мы знаем давление \( P_2 \) в состоянии "2". Теперь мы можем рассчитать работу газа на первом участке кривой, используя интеграл:
\[ W_1 = \int_{V_1}^{V_2} P(V) dV \]
\[ W_1 = \int_{V_1}^{V_2} \frac{P_2}{V} dV \]
\[ W_1 = \int_{V_1}^{V_2} \frac{20775}{V} dV \]
Интегрируя это уравнение, мы получим:
\[ W_1 = 20775 \cdot \ln\left(\frac{V_2}{V_1}\right) \]
Теперь, чтобы рассчитать работу газа на втором участке кривой, от состояния "2" до состояния "3", нам необходимо определить, какой тип процесса происходит.
Из графика видно, что объем и давление газа не меняются на этом участке, что означает, что происходит изохорический процесс (процесс при постоянном объеме). В этом случае работа газа равна нулю, так как
\[ W_2 = P_2(V_3 - V_2) = 0 \]
Наконец, чтобы рассчитать работу газа на третьем участке кривой, от состояния "3" до состояния "4", мы также должны определить тип процесса. Из графика видно, что давление газа увеличивается, а объем остается постоянным. Это означает, что происходит изобарный процесс (процесс при постоянном давлении).
У нас есть давление в состоянии "4", которое можно найти, зная, что \( P_4 = P_3 \):
\[ P_4V_4 = P_3V_3 \]
\[ P_4 = \frac{P_3V_3}{V_4} \]
Теперь мы можем рассчитать работу газа на третьем участке кривой, используя интеграл:
\[ W_3 = \int_{V_3}^{V_4} P(V) dV \]
\[ W_3 = \int_{V_3}^{V_4} P_4 dV \]
\[ W_3 = P_4(V_4 - V_3) \]
Таким образом, работа газа на третьем участке кривой равна:
\[ W_3 = P_4(V_4 - V_3) \]
В итоге, общая работа газа в этом процессе будет равна сумме работ на каждом участке кривой:
\[ W_{\text{общ.}} = W_1 + W_2 + W_3 \]
Подставляя значения, мы можем рассчитать работу газа в этом процессе.
Таким образом, решение данной задачи будет включать:
1. Определение давления в состоянии "2" с использованием уравнения состояния \( PV = nRT \).
2. Расчет работы газа на первом участке кривой, от состояния "1" до состояния "2", с использованием интеграла \( W = \int_{V_1}^{V_2} P(V) dV \).
3. Определение типа процесса на втором участке кривой, от состояния "2" до состояния "3", и установление, что работа газа равна нулю в этом случае.
4. Определение давления в состоянии "4" с использованием уравнения состояния \( P_4 = \frac{P_3V_3}{V_4} \).
5. Расчет работы газа на третьем участке кривой, от состояния "3" до состояния "4", с использованием интеграла \( W = \int_{V_3}^{V_4} P(V) dV \).
6. Расчет общей работы газа в этом процессе, суммируя работы на каждом участке кривой.