1. Физика
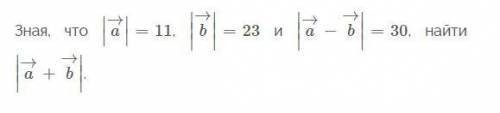
  2. Решите задачку по физике Во вложении

Решите задачку по физике Во вложении


Решите задачку по физике Во вложении

FireFlyWasDeadBefore FireFlyWasDeadBefore    3   31.08.2020 20:27    3

Ответы
Монокль Монокль  15.10.2020 16:31

20

Объяснение:

Просто вспомним правило параллелограмма (см. рисунок). Очевидно, что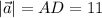 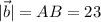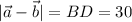\displaystyle |\vec{a}|=AD=11, \displaystyle |\vec{b}|=AB=23, \displaystyle |\vec{a}-\vec{b}|=BD=30, тогда искомый модуль суммы равен длине второй диагонали АС, найти ее можно, воспользовавшись тождеством параллелограмма:

\displaystyle AC^2+BD^2=2(AD^2+AB^2)

\displaystyle |\vec{a}+\vec{b}|=AC=\sqrt{2(AD^2+AB^2)-BD^2}=\sqrt{2*(11^2+23^2)-30^2}=

=\sqrt{400}=20.


Решите задачку по физике Во вложении
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
ykropmen ykropmen  23.06.2019 20:00
Решить 1)как связаны между собой изменение потенциальной и кинетической энергии при свободном падении тела? 2)от чего зависит потенциальная энергия тела в поле силы тяжести?...
natalikc natalikc  16.03.2020 07:24
Камень свободно падает с высоты 1200 м. Найти время падения и конечную скорость. Какой путь пройдет камень за последнюю секунду своего падения....
kokoriki kokoriki  16.03.2020 07:24
На первичную обмотку трансформатора, имеющую 120 витков, подано напряжение 220 В. Вторичная обмотка имеет 320 витков. Определи напряжение на зажимах вторичной обмотки и...
Alinok99 Alinok99  16.03.2020 07:23
Участок цепи состоит из двух последовательно соединенных резисторов. Напряжение на первом резисторе 8B. Определите напряжение на втором резисторе, если напряжение на участке...
vsevolod2013 vsevolod2013  16.03.2020 07:23
физика 7 класс.Задание. Трансатлантический лайнер Титаник , построенный в 1911 году, имел возмещение 46328 т, длину 269 м, ширину 9 28,2 м, скорость 46,3 км/ч. 1. Верно...
Moran1 Moran1  16.03.2020 07:23
Определить высоту подвеса передающей антенны телецентра, обеспечивающую приём в зоне радиусом 60 км. Высота подвеса приёмных антенн 10 м...
ахаххахаха11 ахаххахаха11  16.03.2020 07:21
Нужно решить задания от 8 и до...
Andreyvko1 Andreyvko1  16.03.2020 07:21
престать ответы с решением каждого задания теста буквы мне не нужны....
en228 en228  16.03.2020 07:19
Объясните первый закон фотоэффекта словами. Можно с какими-нибудь тупыми примерами, но чтоб понятно было. Очень нужно...
nastyazhovnirenko nastyazhovnirenko  16.03.2020 07:18
Выбери формулу вещества, с которого можно осуществить превращение: Ag3PO4→H3PO4. 1)AgNO3 2)CH4 3)H2SO4 4)NaOH...

Популярные вопросы