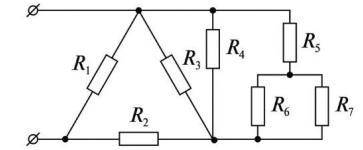
решить задачи много : Задача 1: Определить эквивалентное сопротивление цепи (рисунок 1), состоящей из резисторов, каждый из которых по 7 Ом.
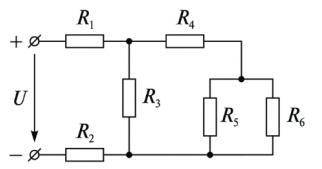
Задача 2: Рассчитать электрическую цепь (рисунок 2) методом
эквивалентных сопротивлений, и проверить правильность решения, составив уравнение баланса мощностей. Параметры цепи: каждый резистор имеет сопротивление 5 Ом, напряжение питающей сети 100 В.
Другие вопросы по теме Физика
Популярные вопросы
- на какое число нужно умножить две части другого примера системы чтобы достать у...
2 - , БУДУ ОЧЕНЬ БЛАГОДАРНА‼️ текст и задания на фото....
1 - мне очень надо все что есть...
2 - Можете ответить на 2 вариант...
3 - Составь сообшение значение легкой промышленности в жизни людей ....
3 - сколько водяного пара содердит 1м2 при температуре 10°с, если его относительная...
1 - Запишите и выделите в словах общий корень. куст, кустик, кусток, кусточек; кот,...
1 - Масова частка Оксигену в одноатомному спирті 21,62%. Знайдіть молекулярну і запишіть...
1 - 2. Як ви думаєте, чи правомірним є називати українську культуру XVII-XVIII ст....
1 - В чем актульность рассказа М.А. Шолохова Судьба человека для нас, живущих в эпоху...
2
Для решения данной задачи, мы должны определить общее сопротивление цепи, состоящей из резисторов, каждый из которых имеет сопротивление 7 Ом.
Сначала, посмотрим на рисунок 1 и запишем информацию о заданной цепи:
- У нас есть 3 резистора: R1, R2 и R3, каждый из которых имеет сопротивление 7 Ом.
Для того чтобы найти эквивалентное сопротивление цепи, мы можем использовать формулу для параллельного соединения резисторов:
1/Req = 1/R1 + 1/R2 + 1/R3,
где Req - эквивалентное сопротивление цепи.
Подставляем известные значения:
1/Req = 1/7 + 1/7 + 1/7,
Упрощаем дроби:
1/Req = 3/7,
Теперь находим обратное значение:
Req = 7/3 Ом.
Таким образом, эквивалентное сопротивление цепи, состоящей из трех резисторов по 7 Ом каждый, равно 7/3 Ом.
Задача 2: Расчет электрической цепи методом эквивалентных сопротивлений.
В данной задаче, нам нужно рассчитать электрическую цепь (рисунок 2) методом эквивалентных сопротивлений и проверить правильность решения, составив уравнение баланса мощностей.
Смотрим на рисунок 2 и записываем информацию о заданной цепи:
- У нас есть 4 резистора: R1, R2, R3 и R4, каждый из которых имеет сопротивление 5 Ом.
- Напряжение питающей сети составляет 100 В.
Шаг 1: Расчет эквивалентного сопротивления для резисторов R3 и R4, которые соединены последовательно:
Req34 = R3 + R4 = 5 + 5 = 10 Ом.
Шаг 2: Расчет эквивалентного сопротивления для резисторов R2 и Req34, которые соединены параллельно:
1/Req234 = 1/R2 + 1/Req34,
1/Req234 = 1/5 + 1/10,
1/Req234 = 2/10 + 1/10,
1/Req234 = 3/10.
Теперь находим обратное значение:
Req234 = 10/3 Ом.
Шаг 3: Расчет эквивалентного сопротивления для резистора R1 и Req234, которые соединены параллельно:
1/Req1234 = 1/R1 + 1/Req234,
1/Req1234 = 1/5 + 1/(10/3),
1/Req1234 = 1/5 + 3/10,
1/Req1234 = 2/10 + 3/10,
1/Req1234 = 5/10.
Теперь находим обратное значение:
Req1234 = 10/5 = 2 Ом.
Таким образом, эквивалентное сопротивление электрической цепи, состоящей из 4 резисторов по 5 Ом каждый, равно 2 Ом.
Проверка правильности решения:
Для того, чтобы проверить правильность решения, составим уравнение баланса мощностей.
Мощность P, потребляемая цепью, можно вычислить по формуле P = U^2 / R, где U - напряжение, R - сопротивление.
Мощность P1, потребляемая резистором R1, будет равна P1 = U^2 / R1 = 100^2 / 5 = 2000 Вт.
Мощность P234, потребляемая резисторами R2, R3 и R4, будет равна P234 = U^2 / Req234 = 100^2 / (10/3) = 3000 Вт.
Мощность P1234, потребляемая всей цепью, будет равна P1234 = U^2 / Req1234 = 100^2 / 2 = 5000 Вт.
Проверим, что сумма мощностей P1 и P234 равна мощности P1234:
P1 + P234 = 2000 + 3000 = 5000 Вт, что соответствует мощности P1234.
Таким образом, мы убедились в правильности решения, так как мощность, потребляемая всей цепью, равна сумме мощностей, потребляемых каждым из резисторов.