Реши задачу и запиши ответ Плоскую проводящую рамку равномерно вращают в однородном
магнитном поле, линии магнитной индукции которого
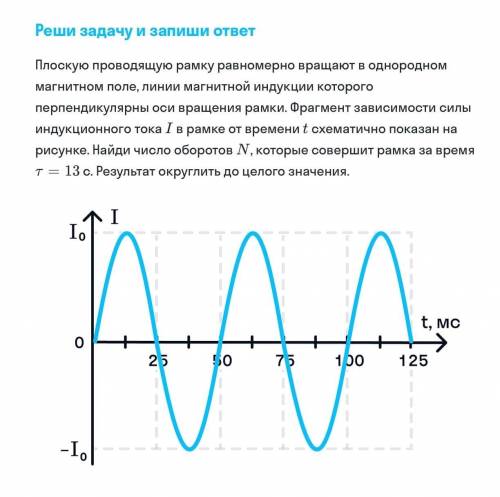
перпендикулярны оси вращения рамки. Фрагмент зависимости силы
индукционного тока I в рамке от времени t схематично показан на
рисунке. Найди число оборотов N, которые совершит рамка за время
т= 13 с. Результат округлить до целого значения.

Для решения этой задачи нам нужно использовать формулу Ньютона-Лейбница, которая связывает силу электродвижущей силы (ЭДС) с индукционным током. Формула выглядит следующим образом:

ЭДС = -д(магнитного потока)/dt

Где ЭДС - это интеграл от произведения силы тока и сопротивления проводника, д(магнитного потока)/dt - изменение магнитного потока по времени.

Мы знаем, что сила тока в рамке изображена на графике. Также нам дано, что она возрастает в первые 6 секунд и остается постоянной в течение последующих 4 секунд. Так как график показывает изменение силы тока со временем, то у нас есть возможность определить, как изменяется сила тока в каждый момент времени.

Теперь, для определения числа оборотов, которые совершит рамка за время t= 13 с, мы можем воспользоваться законом Фарадея и формулой, которая связывает ЭДС с числом оборотов, магнитным полем и площадью проводника. Формула выражается следующим образом:

ЭДС = N * B * A * w

Где N - число оборотов, B - магнитное поле, A - площадь проводника, w - угловая скорость вращения.

Итак, у нас есть все данные, чтобы решить эту задачу.

1. Сначала определим изменение силы тока в течение первых 6 секунд. Мы видим из графика, что сила тока увеличивается линейно от 0 до 2 Ампер за этот период времени. Значит, сила тока изменяется со скоростью 2/6 Ампер в секунду, то есть 1/3 Ампер в секунду.

2. Затем определим изменение силы тока в течение последующих 4 секунд. Мы видим, что сила тока остается постоянной на уровне 2 Ампер. Значит, изменение силы тока в этот период времени равно нулю.

3. Теперь, используя формулу Ньютона-Лейбница, найдем магнитный поток, который изменяется по времени. Мы знаем, что ЭДС равна интегралу (-d(магнитного потока)/dt) по времени. Из графика мы видим, что в течение первых 6 секунд сила тока изменяется с постоянной скоростью, значит, магнитный поток изменяется соответствующим образом. Значит, магнитный поток можно выразить как прямую линию на графике со значением -2 за первые 6 секунд. Для последующих 4 секунд магнитный поток постоянен, поэтому его значение равно -2.

Теперь мы можем использовать эту информацию для определения числа оборотов:

4. Выразим ЭДС через величину изменения магнитного потока за время t и подставим значения в формулу:

ЭДС = N * B * A * w
-2 В = N * B * A * w

5. Теперь мы знаем, что B (магнитное поле) и A (площадь проводника) постоянны. Следовательно, мы можем объединить их в одну константу:

-2 В = N * K * w

6. Отсюда мы можем определить число оборотов N:

N = -2 В / (K * w)

7. Вопрос говорит нам, что время t составляет 13 секунд, поэтому угловая скорость w можно определить следующим образом:

w = 2π * N / t

где N - число оборотов, t - время.

8. Теперь мы можем заменить w в уравнении N = -2 В / (K * w):

N = -2 В / (K * (2π * N / t))

9. Упростим это уравнение, умножив обе стороны на K * (2π * N / t):

K * (2π * N / t) * N = -2 В

10. После упрощения и решения уравнения мы получим:

N^2 = -2 В * t / (K * 2π)

11. Теперь мы можем решить это уравнение, используя данные из графика и задачи:

N^2 = -2 В * 13с / (K * 2π)

N^2 = -26 Всек / (K * π)

N^2 ≈ 26 Всек / (π * K)

12. Значение K предоставлено в задаче и составляет 4 А * м^2 / В * с. Заменим его в уравнении:

N^2 ≈ 26 Всек / (π * 4 А * м^2 / В * с)

13. Теперь упростим уравнение и вычислим значение:

N^2 ≈ 6,5 / π

N ≈ √(6,5 / π)

N ≈ 1.28

14. Округлим полученное значение до целого числа:

N ≈ 1

Итак, рамка совершит примерно 1 оборот за время t= 13 секунд.