Равноплечный рычаг закреплён на опоре высоты h = 0,5 м и массы m = 10 кг. между обоими концами рычага и потолком закреплены пружины с жёсткостями k1 = 25 н/м и k2 = 15 н/м. длина обеих пружин в нерастянутом состоянии равна x0 = 0,4 м. высота потолка равна h = 1,5 м. вся система находится в равновесии. с какой силой f опора давит на пол? считайте, что пружины невесомы и вертикальны.
! здесь 19935!
Другие вопросы по теме Физика
Популярные вопросы
- Знатні люди у польщі та великому князівстві литовському об єднані в єдину...
1 - Даю 20- ! Дайте хронологию на древний мир и античные времена, пожайлуста,...
1 - бірінші күні жұмысшылар бригадасы жолдын 5/14 бөлігін жөндеді ,ал екінші күні...
3 - По какому признаку элементы размещены в периодической таблице? уменьшение...
3 - Возможно ли образование пептидной связи между α-амино группой одной аминокислоты...
3 - Укажи предложение с вводной конструкцией, обозначающей источник сообщения....
2 - 12,444:(7-2,92)+1,03*(13,65-3)=?...
3 - 4.запишите формулу U движения по окружности 5. по какой траектории движется...
3 - В чем тайна певца в стихотворении «Арион»?...
3 - Әке мен бала Біра ертіп, егіннен жаяу кайтып келе жатып, жолда қалған аттың...
2
ответ: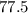 Н
Н
Объяснение:
Полное условие задачи (с рисунком) представлено во вложении - рис. 1
Дано:
-------------------
Вначале несколько слов в стиле описательного момента.
Согласно условию задачи, если у нас рычаг равноплечный и находиться в состоянии покоя, то из за того что пружины, подвешенные к его концам, растянуты, а их жесткости не равны между собой, можно сделать вывод, что их длинны, аналогично, не равны друг другу. Из за того что жесткость пружины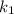 больше чем у
больше чем у 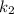 , то пружина
, то пружина
Где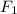 - сила упругости пружины жесткостью
- сила упругости пружины жесткостью 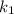
Где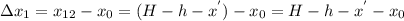
Как было отмечено раньше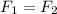
Теперь пусть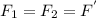
Отсюда
Ну или
Что еще раз подтверждает наши соображения
Если считать рычаг вместе с опорой одним целым телом то в проекции на ось