Радиус-вектор материальной точки относительно начала координат изменяется со временем по известному закону, в котором i и j — орты осей Х и У. Найти: а) уравнение траектории и изобразить ее графически; б) проекции скорости на оси координат; в) зависимости от времени

векторов скорости и ускорения и модули этих величин в момент времени t1.

Закон изменения радиуса-вектора: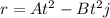

A=16м/с^2

B=12м/с

t1=0,1с

Сначала рассмотрим заданный закон изменения радиус-вектора:
r = At^2 - Bt^2 j,

где A = 16 м/с^2 и B = 12 м/с.

а) Чтобы найти уравнение траектории и изобразить ее графически, нужно найти проекции радиус-вектора на оси координат X и Y.

Проекция радиус-вектора r на ось X: r_x = At^2,
Проекция радиус-вектора r на ось Y: r_y = -Bt^2.

Теперь мы можем записать уравнение траектории:
x = At^2,
y = -Bt^2.

Для графического изображения траектории нужно построить график этих уравнений на плоскости координат.

б) Чтобы найти проекции скорости на оси координат, нужно взять производные проекций радиус-вектора по времени.

Проекция скорости на ось X: v_x = 2At,
Проекция скорости на ось Y: v_y = -2Bt.

в) Чтобы найти зависимости от времени векторов скорости и ускорения, а также их модулей в момент времени t1 = 0.1 с, нужно подставить значение времени в выражения для проекций скорости и ускорения.

Вектор скорости в момент времени t1:
v = v_x i + v_y j = 2A t1 i - 2B t1 j.

Вектор ускорения в момент времени t1:
a = dv/dt = 2A i - 2B j.

Модуль вектора скорости в момент времени t1:
|v| = sqrt((v_x)^2 + (v_y)^2) = sqrt((2A t1)^2 + (-2B t1)^2).

Модуль вектора ускорения в момент времени t1:
|a| = sqrt((2A)^2 + (-2B)^2).

Теперь остается только численно подставить значения A, B и t1 в эти выражения, чтобы получить конкретные числовые значения.