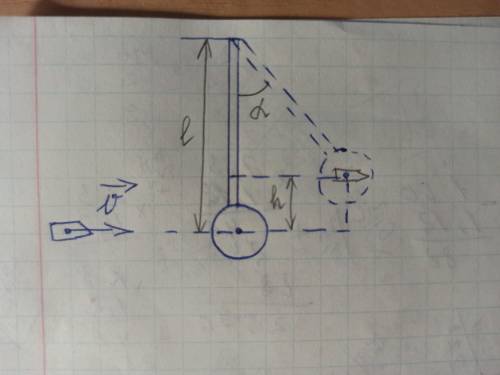
Пуля, летящая горизонтально со скоростью V, попадает в шар, подвешенный на невесомом жёстком стержне, и застревает в нем. Масса пули – m, масса шара – М. Расстояние от центра шара до точки подвеса стержня – l. От удара пули стержень с шаром отклонился на угол α, поднявшись на высоту h. Принять g=10 м/с2. m=4,6г
V=670 м/c
l=1,51м
α=5°
Найти высоту h и массу шара M.

Для решения данной задачи воспользуемся законом сохранения импульса и законом сохранения механической энергии.

Закон сохранения импульса:

p1 = p2,

где p1 - импульс пули до столкновения (так как пуля летит горизонтально, импульс в вертикальном направлении равен нулю),
p2 - импульс системы пуля + шар после столкновения.

Импульс - это произведение массы на скорость:

p1 = m * V,
p2 = (m + M) * u,

где u - скорость системы пуля + шар после столкновения.

Зная, что пуля застревает в шаре, можем записать следующее:

m * V = (m + M) * u.

Теперь приступим к закону сохранения механической энергии.

Первоначальная механическая энергия системы равна кинетической энергии пули:

E1 = (m * V^2) / 2.

После столкновения, при отклонении стержня на угол α, механическая энергия системы равна потенциальной энергии поднятой на высоту h массы шара и потенциальной энергии поднятой на высоту l-h массы стержня и пули:

E2 = (M * g * h) + ((m + M) * g * (l - h)).

Из закона сохранения механической энергии следует:

E1 = E2.

Таким образом, у нас есть два уравнения:

m * V = (m + M) * u,
(m * V^2) / 2 = (M * g * h) + ((m + M) * g * (l - h)).

Теперь решим систему данных уравнений.

Из первого уравнения можем выразить ускорение u через скорость пули V:

u = (m * V) / (m + M).

Подставим полученное значение во второе уравнение:

(m * V^2) / 2 = (M * g * h) + ((m + M) * g * (l - h)).

Раскроем скобки и приведем подобные слагаемые:

m * V^2 / 2 = M * g * h + m * g * (l - h) + M * g * (l - h).

Далее, приведем подобные слагаемые:

m * V^2 / 2 = M * g * h + m * g * l - m * g * h + M * g * l - M * g * h.

Сократим m * g * h с двух сторон уравнения:

m * V^2 / 2 = M * g * h + m * g * l - M * g * h.

Перенесем все слагаемые с M на одну сторону уравнения:

M * g * h - M * g * h = m * V^2 / 2 - m * g * l.

Сокращаем M * g * h - M * g * h:

0 = m * V^2 / 2 - m * g * l.

Учитывая данные задачи, получаем:

0 = (4.6 * 10^-3 * 670^2) / 2 - 4.6 * 10^-3 * 10 * 1.51.

Решив данное уравнение, найдем значение h.
Далее, используя найденное значение h, мы сможем найти значение M с помощью первого уравнения.