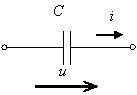
При напряжении u(t)=100sin(314t) В начальная фаза тока i(t) в ёмкостном элементе C составит… а) p/2 рад б) -p/4 рад в) 0 рад г) 3p/4 рад

Для решения данной задачи нужно использовать понятие фазового сдвига между напряжением и током в емкостном элементе.

В емкостном элементе ток отстает по фазе от напряжения на 90 градусов или на пи/2 радиан. То есть, начальная фаза тока i(t) в емкостном элементе C будет равна пи/2 радиан.

Это можно объяснить следующим образом:

Емкостный элемент C обладает реактивным сопротивлением, которое зависит от угловой частоты сигнала. Если на емкостном элементе C приложено синусоидальное напряжение u(t) = Usin(ωt), то сила тока i(t) в текующий момент времени можно выразить формулой:

i(t) = C * d(u(t))/dt

Где C - ёмкость элемента C, d(u(t))/dt - производная по времени от напряжения u(t).

Дифференцируя синусоидальную функцию по времени, получим следующее:

du(t)/dt = ωUcos(ωt)

Где ω - угловая скорость (ω = 2πf, где f - частота сигнала).

Дифференцируя результат по времени еще раз, получаем:

d(du(t)/dt)/dt = -ω^2Usin(ωt)

То есть, итоговая формула для силы тока i(t) будет:

i(t) = -ω^2Usin(ωt)

Если подставить значение синусоидального сигнала u(t) = Usin(ωt), в котором u(t) = 100sin(314t), то получим:

i(t) = -ω^2Usin(ωt) = -ω^2 * 100sin(314t)

Таким образом, фазовый сдвиг составляет пи/2 радиан или 90 градусов. Также можно заметить, что коэффициент перед синусом отрицательный, что означает, что ток отстает от напряжения на 90 градусов по фазе.

Ответ: а) p/2 рад