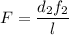Предмет находится на расстоянии l=60 см от экрана. используя тонкую линзу, на экране получают сначала уменьшенное изображение предмета, а затем, перемещая. линзу ,-увеличенное изображение, которое в г=2 раза больше первого. определите фокусное расстояния f линзы.
Другие вопросы по теме Физика
Популярные вопросы
- Потрібно скласти план до твору енеїда ,як його складать? ( через цитати,чи звичайно)...
1 - Сколько атомов содержится в 80 г кальция? решите решебник автор радецкии а.м....
2 - Как спросить по- могу ли я верить джону смиту ?...
2 - Нужно. в двумерном массиве размерности nxn найти сумму положительных элементов...
2 - Вбуквенное ателье пришли слова в звуковых костюмах и попросили подобрать им буквенный...
2 - Пользуясь и политической картами мира , охарактеризуйте геополитическое положение...
1 - План рассказа о герое.о маше троекуровой и о самом троекуровом! (по роману дубровского)...
1 - Отгадайте слова: 1. сог., мягк., глух., парн.,+ глас.+кар+согл, мягк., зво.н,...
2 - 1. дан угол с вершиной в точке s и точка m внутри него. провести через точку m...
3 - Почему при образовании ковалентной связи расстояние между атомами строго определенно?...
2
ответ: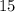 см
см
Объяснение:
Дано:
---------------
Из условия становиться понятно что мы имеем дело в этой задаче с собирающей линзой, действительным изображением и предметом "на экране получают сначала уменьшенное изображение предмета, а затем, перемещая. линзу ,-увеличенное изображение"
Тогда формула "тонкой линзы" имеет вид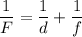 ⇒
⇒ 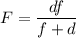
Согласно условию задачи "предмет находится на расстоянии l=60 см от экрана", тогда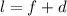 (отсюда
(отсюда 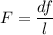 (0)) а также т.к. в этой задаче перемещают только линзу, то
(0)) а также т.к. в этой задаче перемещают только линзу, то 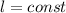 ⇒
⇒ 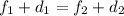
Мы знаем что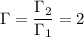 ("увеличенное изображение, которое в Г=2 раза больше первого.")
("увеличенное изображение, которое в Г=2 раза больше первого.")
В общем случае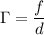 ⇒ в нашем случае при
⇒ в нашем случае при 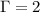 ;
; 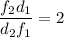 (1.1)⇒
(1.1)⇒ 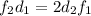 (1.2)
(1.2)
Т.к.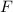 и
и 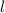
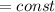 , то
, то 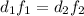 (2) ⇒
(2) ⇒ 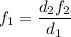 (3)
(3)
Поставляя уравнение (3) в (1.2) получим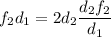 ⇒
⇒ 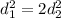 ⇒
⇒ 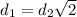 (4)
(4)
Поставляя уравнение (4) в (2) получим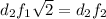 ⇒
⇒ 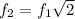 или
или 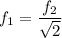 (5)
(5)
Согласно уравнению (1.1)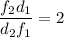
Подставляя уравнение (4) в (1.1) получим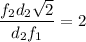 ⇒
⇒ 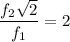 ⇒
⇒ 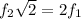 , т.к.
, т.к. 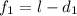 , а
, а 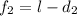 ,то
,то 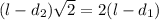 учитывая уравнение (4) получим
учитывая уравнение (4) получим 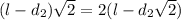 ⇒
⇒ 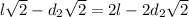 ⇒
⇒  ⇒
⇒ 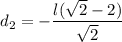
Тогда т.к.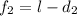 , то
, то 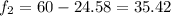 см
см
Из уравнения (0) следует что