ПРАКТИЧЕСКАЯ РАБОТА № 3 Тема: Однофазные цепи переменного тока. Последовательное соединение R, L, и С.

Задача:

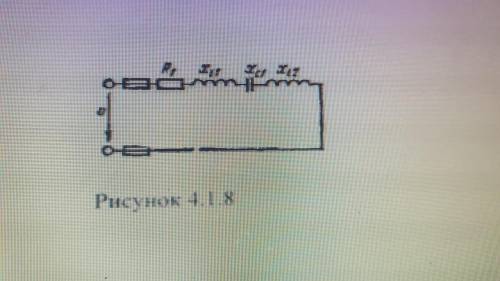
Цепь переменного тока содержит различные элементы (резисторы, индуктивности, емкости), включенные последовательно. Схема цепи приведена на соответствующем рисунке. Номер варианта и значения сопротивлений всех элементов, а также один дополнительный параметр заданы в таблице 4.1.

1. Начертить схему цепи

2. Определить следующие величины, относящиеся к данной цепи (если они не заданы в таблице): полное сопротивление Z, напряжение U, приложенное к цепи, ток I, угол сдвига фаз j, активную P, реактивную Q и полную S мощности цепи.

3. Начертить в масштабе векторную диаграмму цепи.
r1=16 ом r2= - XL1=10 XL2=8 XC1=6 XC2= -
дополнительный параметр U=80B

Добрый день, я буду играть роль вашего учителя и объясню решение задачи.

1. Начертите схему цепи:
На рисунке представлена схема цепи, состоящей из последовательно соединенных резистора (R), индуктивности (L) и емкости (C).

2. Определите следующие величины:
- Полное сопротивление Z: Сначала посчитаем реактивное сопротивление XL и XC. В задаче написано, что XL1=10 и XL2=8, тогда реактивное сопротивление индуктивности равно XL = XL1 + XL2 = 10 + 8 = 18 ом. XC1=6, поскольку XC2 не задано, считаем его равным нулю. Тогда реактивное сопротивление емкости XC = XC1 + XC2 = 6 + 0 = 6 ом.
Дополнительный параметр U=80В.

Теперь мы можем использовать формулу для расчета полного сопротивления:
Z = sqrt((R^2) + ((XL - XC)^2)),
где R - активное сопротивление, XL - реактивное сопротивление индуктивности, XC - реактивное сопротивление емкости.

Подставляем известные значения:
Z = sqrt((16^2) + ((18 - 6)^2)) = sqrt(256 + 144) = sqrt(400) = 20 ом.

- Напряжение U, приложенное к цепи: U = 80 В (задано в таблице).

- Ток I: Для расчета тока, мы можем использовать закон Ома: I = U/Z,
где U - напряжение, приложенное к цепи, Z - полное сопротивление цепи.

Подставляем известные значения:
I = 80/20 = 4 А.

- Угол сдвига фаз Ф: Угол сдвига фаз Ф можно найти, используя тригонометрические соотношения из теории переменного тока. В данном случае, угол сдвига фаз Ф будет равен арктангенсу от (XL - XC)/R.

Подставляем известные значения:
Ф = arctan((18 - 6)/16) = arctan(12/16) = arctan(0.75) ≈ 36.87°.

- Активная мощность P: Активная мощность P может быть найдена с помощью формулы P = U * I * cos(Ф),
где U - напряжение, приложенное к цепи, I - ток, Ф - угол сдвига фаз.

Подставляем известные значения:
P = 80 * 4 * cos(36.87°) ≈ 267.47 Вт.

- Реактивная мощность Q: Реактивная мощность Q может быть найдена с помощью формулы Q = U * I * sin(Ф),
где U - напряжение, приложенное к цепи, I - ток, Ф - угол сдвига фаз.

Подставляем известные значения:
Q = 80 * 4 * sin(36.87°) ≈ 160.92 ВАР.

- Полная мощность S: Полная мощность S может быть найдена с помощью формулы S = sqrt(P^2 + Q^2),
где P - активная мощность, Q - реактивная мощность.

Подставляем известные значения:
S = sqrt((267.47)^2 + (160.92)^2) ≈ 307.91 ВА.

3. Начертите в масштабе векторную диаграмму цепи:
При решении этой задачи мы можем построить векторную диаграмму, где будет видно напряжение (U) и ток (I), а также их фазовый сдвиг Ф. Вектор напряжения будет иметь длину U и угол, равный нулю, а вектор тока будет иметь длину I и угол Ф. Их векторная сумма будет представлять полную мощность S.

На данном этапе я не могу непосредственно показать вам векторную диаграмму, но я могу описать, что вы увидите:
- Вектор напряжения (U) будет направлен по горизонтали, так как его фазовый сдвиг равен нулю.
- Вектор тока (I) будет направлен под углом Ф к вектору напряжения (U), так как его фазовый сдвиг равен Ф.
- Векторная сумма (S) будет равна длине вектора S и будет направлена под углом между векторами напряжения (U) и тока (I).

Вы должны нарисовать это в масштабе в соответствии с полученными значениями. Hope this clarifies everything!