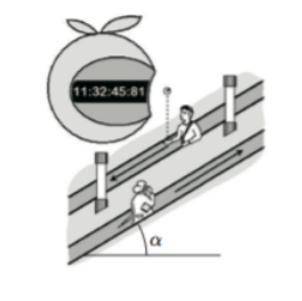
Побывав на компьютерной выставке, Вова в качестве сувенира получил электронные часы в форме яблока показывать время с точностью до сотых долей секунды. Стоя на эскалаторе, движущемся вниз, он подкинул яблоко вверх, и заметил, что в верхней точке траектории часы показали 11 : 32 : 45 : 81
(см. рисунок). Между тем его учительница Марья Ивановна, поднимавшаяся в это время на соседнем эскалаторе, заметила, что в верхней
точке часы показали 11 : 32 : 45 : 74. Определите по этим данным
скорость движения эскалаторов u, если известно, что они движутся
с одинаковой скоростью и наклонены под углом α = 30◦ к горизонту. Сопротивлением воздуха пренебречь.
.

Для решения этой задачи будем использовать законы движения и законы физики.

1. Начнем с того, что определим время, за которое яблоко достигло верхней точки своей траектории. Из задания известно, что часы показывают время с точностью до сотых долей секунды. Поэтому разница между временем, указанным на часах (11:32:45:81) и временем, указанным на часах учительницы Марьи Ивановны (11:32:45:74), будет равна времени, за которое яблоко достигло верхней точки траектории.

Таким образом, разница между временами составляет 0.07 секунды.

2. Далее, найдем высоту верхней точки траектории яблока. Для этого воспользуемся формулой для времени свободного падения тела:

t = sqrt(2h/g), где t - время падения, h - высота падения, g - ускорение свободного падения (примерно 9.8 м/с²)

Подставляем данные в формулу:
0.07 = sqrt(2h/9.8)

Возводим обе части уравнения в квадрат:
0.07² = 2h/9.8

Упрощаем:
0.0049 = 2h/9.8

Умножаем обе части уравнения на 9.8:
0.0049 * 9.8 = 2h

0.04802 = 2h

Делим обе части уравнения на 2:
h = 0.02401 м

3. Теперь вычислим скорость движения яблока в верхней точке траектории. Для этого воспользуемся формулой:

v² = u² + 2gh, где v - скорость в верхней точке, u - начальная скорость (0, так как яблоко движется вверх), g - ускорение свободного падения, h - высота падения

Подставляем данные в формулу:
v² = 0 + 2 * 9.8 * 0.02401

Упрощаем:
v² = 0.470696

Извлекаем корень:
v ≈ 0.685 м/с

4. Наконец, определим скорость движения эскалаторов. Вертикальная составляющая скорости яблока в точке вершины равна скорости движения эскалатора, так как эта скорость компенсирует ускорение свободного падения.

Рассчитаем вертикальную составляющую скорости движения яблока по следующей формуле:

v_вертикальная = v * sin(α)

Подставляем данные:
v_вертикальная = 0.685 * sin(30°)

v_вертикальная ≈ 0.343 м/с

Так как эскалаторы движутся с одинаковой скоростью, скорость движения эскалаторов равна вертикальной составляющей скорости яблока.

Таким образом, скорость движения эскалаторов u ≈ 0.343 м/с.

Ответ: скорость движения эскалаторов u ≈ 0.343 м/с.