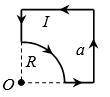
По контуру, представленному на рисунке, течет ток I=10 А. Найти величину и направление индукции магнитного поля в точке O, если сторона квадрата a=35,4 см, а радиус закругленной части R=19,6 см.

Чтобы найти величину и направление индукции магнитного поля в точке O, необходимо применить закон Био-Савара-Лапласа. Этот закон устанавливает, что вектор индукции магнитного поля dВ, создаваемый элементом контура с током, пропорционален векторному произведению вектора тока I на элемент длины ds и обратно пропорционален квадрату расстояния r между элементом и точкой O.

Интегрируя по всем элементам контура, мы получаем полную индукцию B, создаваемую вокруг контура:

B = ∫(dВ) = ∫(k × (ds × I)) / r²,

где k - постоянная пропорциональности.

В данном случае, поскольку квадрат замкнут, полная индукция магнитного поля будет равна векторной сумме индукций магнитных полей, создаваемых каждой стороной и закругленной частью.

Поскольку мы знаем значение тока I (10 А), сторону квадрата a (35,4 см) и радиус закругленной части R (19,6 см), мы можем приступить к решению.

1. Вычислим индукцию магнитного поля, создаваемую каждой стороной квадрата.

Используем формулу, чтобы получить значение индукции магнитного поля (dB) для каждой стороны квадрата:

dB = (k × (ds × I)) / r²,

где r - расстояние от каждого элемента стороны квадрата до точки O. В случае сторон, параллельных осям координат, r будет постоянным (расстояние между элементами и точкой O не изменяется), тогда можно найти индукцию магнитного поля, создаваемую одной стороной и затем умножить ее на количество сторон.

Рассмотрим каждую сторону отдельно:

- Верхняя сторона (a):
r = a/2 (половина стороны),
dB = (k × (ds × I)) / (a²/4),

- Правая сторона (b):
r = R,
dB = (k × (ds × I)) / (R² + a²/4),

- Нижняя сторона (c):
r = a/2,
dB = (k × (ds × I)) / (a²/4),

- Левая сторона (d):
r = R,
dB = (k × (ds × I)) / (R² + a²/4).

2. Вычислим индукцию магнитного поля, создаваемую закругленной частью (e).

Используем формулу для вычисления индукции магнитного поля dB для закругленной части:

dB = (k × (ds × I)) / r²,

где r - расстояние от каждого элемента закругленной части до точки O. Поскольку радиус закругленной части (R) равен 19,6 см, расстояние r будет равно R.

3. Вычислим полную индукцию магнитного поля B.

B = 2 × Bстороны + Bзакругленной_части.

- 2 × Bстороны = 2 × (dBверхняя + dBправая + dBнижняя + dBлевая),
- Bзакругленной_части = dBзакругленная_часть.

4. Найдем значение величины и направления индукции магнитного поля в точке O.

Для рассчета величины и направления индукции магнитного поля в точке O нужно сложить вектора индукции магнитного поля B, создаваемые каждым элементом контура. Направление индукции магнитного поля будет совпадать с направлением пальца правой руки, если положить правую руку таким образом, чтобы большой палец указывал в направлении тока (отрицательное направление заряда к положительному).

Обратите внимание, что в решении данного вопроса используется математическая модель, которая предполагает идеальные условия (например, неучитываем взаимное влияние соседних элементов контура). Поэтому результаты могут несколько отличаться от реальных значений в экспериментальных условиях.