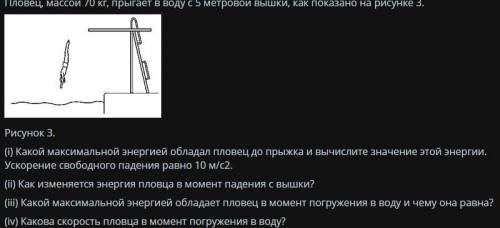
Пловец массой 70кг прыгает в воду с 5 метровой вышки как показано на рисунке

Добрый день!

Для решения этой задачи нам понадобится знание основ физики и формул, связанных с движением тела. Давайте разберемся шаг за шагом.

1. Нам известны следующие данные:
- Масса пловца: 70 кг.
- Высота вышки: 5 м.
- Гравитационное ускорение: примем его равным 9,8 м/с².

2. Теперь посмотрим на рисунок внимательно. Мы видим, что пловец прыгнул с вышки и попал в воду. Нашей задачей будет определить, с какой скоростью он попадет в воду.

3. Решим эту задачу в два этапа. Сначала определим скорость пловца в момент совершения прыжка (на вышке), а затем посчитаем, с какой скоростью он войдет в воду.

4. Для первого этапа нам потребуется использовать закон сохранения энергии. Изначально пловец находится на высоте 5 м над уровнем земли. Запишем эту информацию:
mgh = (70 кг)(9,8 м/с²)(5 м) = 3430 Дж (джоулей).

Итак, полная энергия пловца на вышке равна 3430 Дж.

5. Теперь по-порядку. В момент совершения прыжка все энергия у пловца находится в форме потенциальной энергии (mgh). Когда он начинает падать, эта энергия превращается в кинетическую энергию (½mv²), где v - скорость пловца.

Используя закон сохранения энергии, эквивалент потенциальной энергии нужно приравнять к эквиваленту кинетической энергии.

mgh = ½mv².

6. Теперь мы можем решить это уравнение, чтобы найти значение скорости пловца на вышке. Для этого нам нужно избавиться от одной массы (m) в обоих частях уравнения. Делим обе части на m:

gh = ½v².

Теперь подставляем известные значения и решаем уравнение:

(9,8 м/с²)(5 м) = ½v².

49 = ½v².

7. Чтобы найти скорость пловца на вышке (v), нужно извлечь квадратный корень из обеих частей уравнения:

v² = 49 × 2.

v² = 98.

v ≈ √98.

v ≈ 9,9 м/с.

8. Таким образом, скорость пловца на вышке составляет около 9,9 м/с.

9. Переходим ко второму этапу, где мы должны определить скорость пловца при попадании в воду. Здесь нам понадобятся основы механики падения тела.

10. Пловец падает под действием силы тяжести, поэтому его вертикальное движение подчиняется уравнению свободного падения: h = ½gt², где h - высота падения, g - гравитационное ускорение, t - время падения.

11. Высота падения пловца равна 5 м, поэтому мы можем записать уравнение в следующем виде:

5 м = ½ (9,8 м/с²) t².

12. Теперь решим это уравнение для определения времени падения (t):

5 × 2 = 9,8 t².

10 = 9,8 t².

Делим обе части на 9,8:

t² = 10 ÷ 9,8.

t² ≈ 1,02.

13. Извлекаем квадратный корень из обеих частей:

t ≈ √1,02.

t ≈ 1,01 с.

14. Следовательно, время падения пловца составляет приблизительно 1,01 секунды.

15. Теперь мы можем найти скорость пловца при попадании в воду, используя формулу v = gt. Подставляем известные значения:

v = (9,8 м/с²) × (1,01 с).

v ≈ 9,9 м/с.

16. Таким образом, скорость пловца при попадании в воду также составляет около 9,9 м/с.

Вывод: Пловец с массой 70 кг, прыгая с 5-метровой вышки, войдет в воду со скоростью около 9,9 м/с.