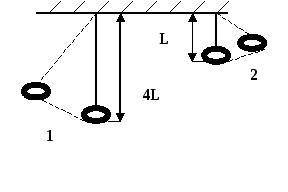
Период колебания второго маятника равен 1 с.Определите период колебаний первого маятника.

Для решения данной задачи нам необходимо воспользоваться математической формулой, связывающей периоды колебаний маятников с их длинами. Формула имеет следующий вид:

T = 2π√(L/g),

где T - период колебаний маятника, L - его длина, π - число пи (примерное значение 3,14), g - ускорение свободного падения (примерное значение 9,8 м/с² на Земле).

Для нахождения периода колебаний первого маятника нам необходимо определить его длину.

Обратимся к картинке, предоставленной в задаче. На ней видно, что второй маятник имеет длину 2L.

Так как период колебаний второго маятника равен 1 с, то можем записать следующее равенство:

1 = 2π√(2L/g).

Теперь выразим L через данное равенство:

1/2 = π√(2L/g).

Разделим обе части уравнения на π:

1/2π = √(2L/g).

Теперь возведем обе части уравнения в квадрат:

(1/2π)² = (2L/g).

Выразим L:

L = ((1/2π)² * g) / 2.

Теперь, когда мы знаем длину первого маятника, можем использовать формулу для нахождения его периода колебаний:

T = 2π√(L/g).

Подставим известные значения:

T = 2π√(((1/2π)² * g) / 2g).

Произведем несколько упрощений:

T = 2π√((1/4π² * g²) / 2g).

T = 2π√(1/8π * g).

T = 2π(1/√8π * √g).

Теперь вычислим значение указанных математических выражений:

√8π = √(8 * 3,14) ≈ √25 ≈ 5.

√g = √9,8 ≈ 3,1.

T ≈ 2 * 3,14 * (1/5 * 3,1) ≈ 6,28 * 0,62 ≈ 3,88 с.

Таким образом, период колебаний первого маятника составляет примерно 3,88 с.