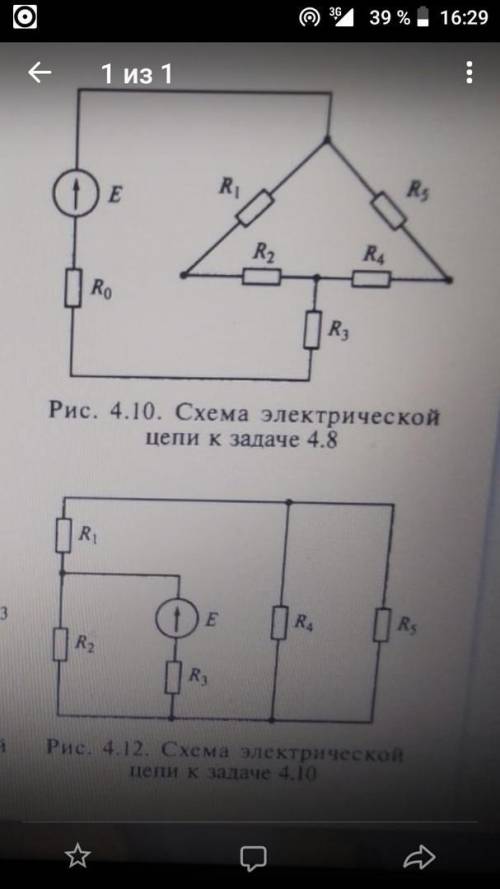
Параметры элементов цепи, показанной на рис. 4.12, имеют следующие значения: Е = 120 В; R1 = 10 Ом; R2 = 40 Ом; R3 = 14 Ом; R4 = 80 Ом; R5 = 50 Ом. Определить токи во всех ветвях цепи

Для определения токов во всех ветвях цепи, мы будем использовать закон Ома и закон Кирхгофа.

Сначала рассмотрим рядом соединенные элементы цепи. В данном случае это R4 и R5. Для ряда соединенных элементов, общее сопротивление рассчитывается путем сложения сопротивлений всех элементов:
R(4+5) = R4 + R5 = 80 Ом + 50 Ом = 130 Ом

Теперь мы можем рассчитать суммарное сопротивление цепи, добавив R(4+5) к параллельно соединенным R2 и R3.
Для параллельно соединенных элементов, общее сопротивление рассчитывается по формуле:
1/R(2+3) = 1/R2 + 1/R3
Инвертируем обе стороны уравнения:
R(2+3) = 1 / (1/R2 + 1/R3)
Подставляем значения R2 и R3:
R(2+3) = 1 / (1/40 Ом + 1/14 Ом)
R(2+3) = 1 / (0.025 Ом^-1 + 0.071 Ом^-1)
R(2+3) = 1 / (0.096 Ом^-1)
R(2+3) = 10.42 Ом

Теперь мы можем рассчитать сопротивление всей цепи, добавив общее сопротивление R(2+3) к последовательно соединенным R1 и R(4+5):
R(1+(2+3+4+5)) = R1 + R(2+3) + R(4+5)
R(1+(2+3+4+5)) = 10 Ом + 10.42 Ом + 130 Ом
R(1+(2+3+4+5)) = 150.42 Ом

Теперь рассчитаем ток в цепи, используя закон Ома:
I = E / R
I = 120 В / 150.42 Ом
I = 0.797 А

Теперь, используя закон Кирхгофа, мы можем рассчитать токи в ветвях цепи:

1. Ветвь с R1:
Ток через R1 будет равен общему току в цепи, так как R1 является единственным элементом на этой ветви.
Ток в ветви R1 = I = 0.797 А

2. Ветвь с R2 и R3:
Распределение тока в параллельно соединенных элементах зависит от их сопротивления - чем меньше сопротивление, тем больше ток через элемент.
Используя закон Ома, мы можем рассчитать ток через R2 и R3:
I(2+3) = E / R(2+3)
I(2+3) = 120 В / 10.42 Ом
I(2+3) = 11.49 А
Ток через R2 будет равен:
I2 = I(2+3) * (R3 / (R2 + R3))
I2 = 11.49 А * (14 Ом / (40 Ом + 14 Ом))
I2 = 4.105 А
Ток через R3 будет равен:
I3 = I(2+3) * (R2 / (R2 + R3))
I3 = 11.49 А * (40 Ом / (40 Ом + 14 Ом))
I3 = 7.384 А

3. Ветвь с R4 и R5:
Ток в ветви с R4 и R5 будет равен общему току в цепи, так как R4 и R5 являются параллельно соединенными элементами.
Ток в ветви R4 и R5 = I = 0.797 А

Итак, итоговые результаты для токов во всех ветвях цепи:
- Ветвь R1: 0.797 А
- Ветвь R2: 4.105 А
- Ветвь R3: 7.384 А
- Ветвь R4 и R5: 0.797 А