1. Физика
  2. Отношение массы Сатурна к массе

Отношение массы Сатурна к массе Земли равно 95, а отношение среднего радиуса Сатурна к среднему радиусу Земли — 12. Чему равен вес спускаемого на Сатурн аппарата массой 254 кг? Считать ускорение свободного падения на поверхности Земли равным 10 м/с2. C дано, решением и ответом

pigaryov2014 pigaryov2014    2   19.08.2020 21:01    124

Ответы
АльбукаеваЗарема АльбукаеваЗарема  15.10.2020 16:04

Дано:

\displaystyle M_c/M_3=95;

\displaystyle R_c/R_3=12;

m=254 кг;

g=10 м/с²;

____________

Найти: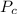 \displaystyle P_c

Сила гравитационного притяжения сообщает телу ускорение свободного падения:

\displaystyle mg=G\frac{mM}{R^2}

\displaystyle g=G\frac{M}{R^2}

Ускорение свободного падения для Земли:

\displaystyle g_3=G\frac{M_3}{R_3^2}

для Сатурна:

\displaystyle g_c=G\frac{M_c}{R_c^2}

Их отношение:

\displaystyle \frac{g_c}{g_3}=G\frac{M_c}{R_c^2}*\frac{R_3^2}{GM_3}=\frac{M_c}{M_3}*\left(\frac{R_3}{R_c} \right)^2 =95*\frac{1}{12^2}=0.66

Таким образом, ускорение свободного падения на Сатурне:

\displaystyle g_c=0.66 g_3=0.66*10=6.6 м/с²

Вес аппарата на Сатурне:

\displaystyle P_c=mg_c=254*6.6=1676 Н

Примечание: в условии задачи допущена неточность, на самом деле отношение радиуса Сатурна к радиусу Земли равно 58232 км/6371 км=9,1

ответ: 1676 Н.

ПОКАЗАТЬ ОТВЕТЫ
Goldcold Goldcold  15.10.2020 16:04

Ускорение свободного падения = G(M/r^2), где М - масса планеты, а r^2 - квадрат ее радиуса. Если хотите - считайте, но проще взять из таблицы, для сатурна это 10,44 м/с^2. Отсюда сила тяжести = масса * ускорение свободного падения = 2850,12 Ньютонов.

КАК-ТО ТАК

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
danielvinixin danielvinixin  26.04.2020 15:27
При равномерном перемещении груза массой 11 кг по наклонной плоскости динамометр, привязанный к грузу, показывал силу, равную 40 Н. Вычисли КПД наклонной плоскости, если...
Пельмешки11 Пельмешки11  26.04.2020 15:27
Очень Посмотрите, какими приборами вы пользуетесь в квартире или в вашей комнате (компьютер, зарядка для телефона, лампочки, телевизор и т.д.). Узнайте мощность этих приборов...
kotovaann2016 kotovaann2016  26.04.2020 15:27
Ребят,учитель сказал что здесь какая-то алгебраическая ошибка...
2710200013 2710200013  26.04.2020 15:27
с этими заданиями, хоть с каким нибудь...
irinar1 irinar1  26.04.2020 15:27
Выберите все верные утверждения о силе тяжести. A.Сила тяжести прямо пропорциональна массе тела. Б.Сила тяжести не зависит от массы тела. В.Сила притяжения двух тел уменьшается,...
SeViK02 SeViK02  26.04.2020 15:27
Автомобіль масою 14 т, рухаючись зі стану спокою, проходить перші 50 м за 10 с . Знайдіть силу тяги, якщо коефіцієнт тертя ковзання дорівнює 0,05?​...
NinCom NinCom  14.05.2020 15:49
Характеристика елементу no 7 за положенням у періодичній системі будь ласка ів...
SofaI SofaI  14.05.2020 15:49
БАГАТО БАЛІВ.Нерухомий блок, ККД якого 85%, використовують, щоб підняти вантаж масою 15 кг на певну висоту. Яку силу прикладають, щоб підняти цей вантаж? Відповідь запишіть...
марьяша18 марьяша18  12.10.2019 09:00
надо, чтобы было (дано, решение, ответ).заранее !...
aish17 aish17  12.10.2019 08:58
Тонкий длинный стержень равномерно заряжен с линейной плотностью 10мккл/м. на продолжении оси стержня на расстоянии 20см от его конца находится точечный заряд, равный...

Популярные вопросы