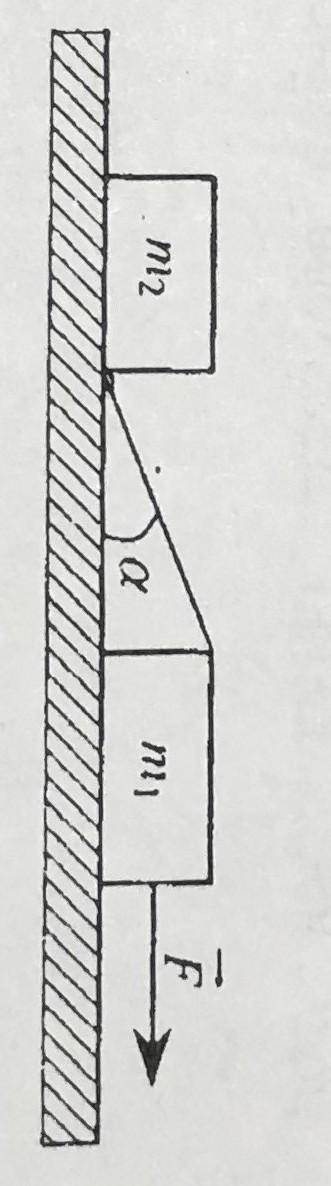
ОТ По гладкому горизонтальному столу движутся 2 кубика, связанные невесомой нитью, под действием горизонтально направленной силы F=16Н. Нить расположена в вертикальной плоскости проходящей через центры кубиков, и образует с горизонтом угол A=30 градусам, который не меняется в процессе их движения. Масса первого кубика m1=4кг, m2=2кг.Найдите силу натяжения нити​

Для решения этой задачи мы можем использовать второй закон Ньютона или закон взаимодействия тел.

Шаг 1: Постановка задачи
У нас есть два кубика (c массами m1 = 4кг и m2 = 2кг), которые движутся по гладкому горизонтальному столу под действием горизонтальной силы F = 16Н. Нить, которая соединяет кубики, расположена в вертикальной плоскости через центры кубиков и образует угол А = 30 градусов с горизонтом.

Шаг 2: Переносим силу натяжения нити на плоскости
Так как нить невесомая, сила натяжения нити (T) будет направлена по нити и будет действовать на оба кубика в направлении плоскости стола. Это означает, что сила натяжения нити будет составлять угол 30 градусов с горизонтом.

F -> (горизонтальная сила направо)
|
| T -> (сила натяжения нити)
|
_________|________________
| | (угол 30 гр.) |
| | |
| | |
| | |
|_________|_________________|
кубик 1 кубик 2

Шаг 3: Разложение силы натяжения по осям
Так как сила натяжения нити образует угол 30 градусов с горизонтом и мы знаем, что нить находится в вертикальной плоскости через центры кубиков, мы можем разложить силу натяжения нити на горизонтальную (Тх) и вертикальную (Ту) компоненты с помощью правил треугольника.

Т
----|-> Тx (горизонтальная компонента)
|
----|
| Ту (вертикальная компонента)
|
|

Шаг 4: Вычисление горизонтальной и вертикальной компоненты силы натяжения (Тх и Ту)
По правилам треугольника мы можем вычислить горизонтальную и вертикальную компоненты силы натяжения:

Тх = Т * cos(A)
Ту = Т * sin(A)

где А - угол между горизонтом и силой натяжения (А = 30 градусов).

Шаг 5: Подстановка известных значений и вычисление силы натяжения (Т)
Теперь мы можем использовать известные значения:
масса первого кубика (m1) = 4кг,
масса второго кубика (m2) = 2кг,
горизонтальная сила (F) = 16Н,
угол (А) = 30 градусов,
гравитационная постоянная (g) ≈ 9.8 м/с².

Мы можем использовать первый закон Ньютона для определения ускорения первого кубика:

F - Тх = m1 * a ---- (1)

Также, ускорение первого кубика (a) и второго кубика (a) будет одинаково (так как они связаны нитью):

a = Ту / m1 = Ту / m2 ---- (2)

Подставляя выражение для Тх из (1) в выражение для a в (2):

F - (Т * cos(A)) = m1 * (Т * sin(A)) / m2

Разрешая относительно силы натяжения (Т):

Т = F * m2 / (m1 * sin(A) + m2 * cos(A))

Теперь мы можем использовать известные значения для вычисления Т:

Т = (16 * 2) / (4 * sin(30) + 2 * cos(30))
Т = 32 / (4 * (1/2) + 2 * (√3/2))
Т = 32 / (2 + 2√3)
Т ≈ 32 / (2 + 2 * 1.732)
Т ≈ 32 / (2 + 3.464)
Т ≈ 32 / 5.464
Т ≈ 5.85 Н

Ответ: Сила натяжения нити (T) ≈ 5.85 Н.