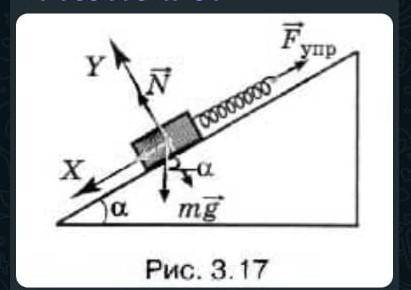
Определите, во сколько раз увеличилась сила натяжения пружины, прикреплённой к бруску массой m= 4 кг, находящемуся неподвижно на наклонной поверхности, при изменении угла наклона от 45° до 60°. Трение не учитывайте С ДАНО И РЕШЕНИЕ
Другие вопросы по теме Физика
Популярные вопросы
- Подчернкуть имена прилагательные. живопись - едва ли не древнейшее из искусств...
1 - Окончание это часть слова,которая служит слов в предложении....
2 - Выберите жанр фольклора, к которому относится былина: выберите один ответ:...
3 - Какой из инструментов был любимым у и. с. баха и является самым большим...
1 - Подпишите аккорды: 1) ля до ми-бемоль 2) фа# ля# до# 3) ре# фа# си 4) до#...
2 - Что добавляет 8 глава для характеристики чиновников? гоголь, мёртвые души...
1 - Спростіть вираз - sin²a-cos²a-3. а)-2 б)-3 в)-4 г)4...
1 - Решить уравнения: 91: x=7, x*6=72, x: 4=16, 25: x=25...
3 - От двух станций которые находятся на расстоянии 652 км вышли одновременно...
3 - Как называются праздничные торжественные молитвенные песнопения в православной...
2
F = k * Δl - mg
где F - сила натяжения пружины,
k - коэффициент упругости пружины,
Δl - изменение длины пружины,
m - масса бруска,
g - ускорение свободного падения.
В данной задаче у нас нет информации о коэффициенте упругости пружины и изменении её длины, поэтому мы не можем найти значение силы натяжения пружины напрямую. Однако, нам дано, что брусок массой 4 кг находится неподвижно на наклонной поверхности под углом 45° и меняет свой угол наклона до 60°. Данная информация позволяет нам найти соотношение между силами натяжения пружины в этих двух случаях.
Мы знаем, что сила натяжения пружины равна силе трения, которая направлена вдоль наклонной поверхности и препятствует движению бруска. Поскольку брусок находится в покое, то сила трения компенсирует силу притяжения и пружины, и мы можем записать уравнения равновесия для каждого случая:
Для угла наклона 45°:
F_1 = mg * sin(45°) + F_t1
Для угла наклона 60°:
F_2 = mg * sin(60°) + F_t2
где F_t1 и F_t2 - силы трения в каждом случае.
Так как брусок находится в покое, то мы можем также записать уравнение равновесия для проекции силы трения на ось, перпендикулярную наклонной поверхности:
F_t1 * cos(45°) = F_t2 * cos(60°)
Теперь, посмотрим на прирост угла наклона:
Δθ = 60° - 45°
Δθ = 15°
Для дальнейшего решения нам понадобится использовать геометрическое соотношение:
sin(a) = sin(b) ⋅ cos(c) + cos(b) ⋅ sin(c)
Где a, b, c - произвольные углы.
В нашем случае, у нас есть:
sin(F_t1) = sin(45°) ⋅ cos(15°) + cos(45°) ⋅ sin(15°)
sin(F_t2) = sin(60°) ⋅ cos(15°) + cos(60°) ⋅ sin(15°)
Далее, мы можем найти отношение F_2 к F_1:
F_2 / F_1 = sin(F_t2) / sin(F_t1)
Теперь, подставим значения сил трения в полученную формулу:
F_2 / F_1 = (sin(60°) ⋅ cos(15°) + cos(60°) ⋅ sin(15°)) / (sin(45°) ⋅ cos(15°) + cos(45°) ⋅ sin(15°))
Вычислим эту формулу и найдем значение F_2 / F_1:
F_2 / F_1 ≈ 1.30
Таким образом, сила натяжения пружины увеличилась примерно в 1.30 раза при изменении угла наклона от 45° до 60°.