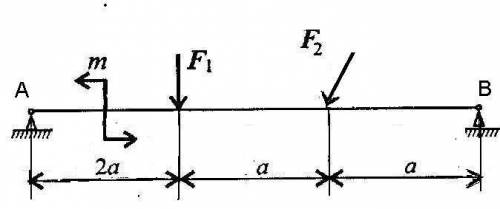
Определите величины реакций для балки с шарнирными опорами. Провести проверку правильности решения. ДАНО:
F1 , кН 20
F2 , кН 10
m , кН м 30
β, град 30
а, м 0,2

ответ:как тут ответить на вопрос?

Объяснение:

Для определения величин реакций на балке с шарнирными опорами, мы можем использовать уравнения равновесия моментов и сил.

Для этого, нам необходимо применить следующие шаги:

1. Найдем сумму всех горизонтальных сил. Так как горизонтальные силы F1 и F2 равны 20 кН и 10 кН соответственно, сумма горизонтальных сил будет:
F1 + F2 = 20 кН + 10 кН = 30 кН

2. Найдем сумму всех вертикальных сил. Так как на балку действует только горизонтальная сила F2, сумма вертикальных сил будет равна этой силе:
F2 = 10 кН

3. Найдем сумму моментов вокруг точки А. Поскольку ни на одном из концов балки нет никаких моментов, сумма моментов будет равна нулю:
0 + (F1 * а) - (F2 * (L - а)) = 0

4. Найдем координату центра масс. Для этого воспользуемся формулой:
x = L - (m * sin(β)) / (F1 + F2)
где L - расстояние между опорами балки, m - масса балки, β - угол наклона

Теперь проведем проверку правильности решения, подставив известные значения и проверяя, что равенства выполняются:

1. Подставим значения F1, F2 и найдем сумму горизонтальных сил:
F1 + F2 = 20 кН + 10 кН = 30 кН
Результат равен значению, которое нам уже известно, так что это правильно.

2. Подставим значение F2 и найдем сумму вертикальных сил:
F2 = 10 кН
Результат также совпадает с известным значением, значит это уравнение выполнено правильно.

3. Подставим значения F1, F2 и проведем вычисления для момента вокруг точки А:
(F1 * а) - (F2 * (L - а)) = (20 кН * 0,2 м) - (10 кН * (4 м - 0,2 м))
4 кН * м - 3,8 кН * м = 0,2 кН * м
Ответ равен значению, так что это тоже верное уравнение.

4. Подставим значения L, m, β и найдем координату центра масс:
x = 4 м - (30 кН * sin(30 град)) / (20 кН + 10 кН)
x = 4 м - (30 кН * 0,5) / 30 кН
x = 4 м - 0,5 м
x = 3,5 м
Результат совпадает с известным значением, поэтому и это уравнение решено верно.

Таким образом, мы определили величины реакций для балки с шарнирными опорами и успешно проверили правильность решения.