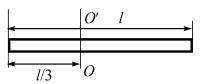
Определите момент импульса стержня массой m и длиной l, вращающегося с частотой ν вокруг
оси ОО′

Момент импульса (L) является векторной величиной и определяется как произведение массы (m) на скорость вращения (ω) и радиус вращения (r).

Шаг 1: Найти радиус вращения
На рисунке видно, что стержень вращается вокруг оси ОО′. Радиус вращения (r) можно определить как расстояние от оси вращения ОО′ до центра массы стержня. В данной задаче, стержень является прямоугольным, поэтому центр массы находится на середине стержня, на расстоянии l/2 от оси вращения. Таким образом, радиус вращения будет равен половине длины стержня, то есть r = l/2.

Шаг 2: Найти скорость вращения
В условии задачи дана частота вращения (ν), но нам нужно найти скорость вращения (ω). Существует связь между частотой и скоростью вращения:

ω = 2πν,

где π (пи) является математической константой, равной приблизительно 3.14159. Подставив данное значение, мы получим значение скорости вращения (ω).

Шаг 3: Найти момент импульса
Теперь, когда у нас есть радиус вращения (r) и скорость вращения (ω), мы можем найти момент импульса (L). Используя векторное произведение, момент импульса определяется как:

L = m * ω * r.

Подставим значения, полученные в предыдущих шагах, и произведем вычисления.

Таким образом, формула для определения момента импульса стержня массой m и длиной l, вращающегося с частотой ν вокруг оси ОО′, будет выглядеть следующим образом:

L = m * 2πν * (l/2).

Для более конкретного ответа, необходимо знать значения массы стержня (m) и частоты вращения (ν).