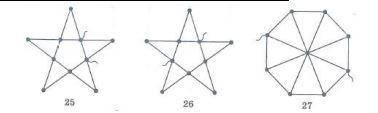
Определите эквивалентные сопротивления проволочных сеток, изображенных на рисунке. Сопротивление каждой ветви любой сетки (вне зависимости от ее длины) равно R.
Другие вопросы по теме Физика
Популярные вопросы
- Почему газы не имеют собственной формы?...
1 - Рассчитайте объем кислорода(н.у), необходимый для сжигания бутана количеством...
2 - Втреугольнике abc, угол а=15, b=75 ch - высота. найдите ав....
1 - Для некоторого предприятия зависимость объема спроса на его продукцию q(едениц...
3 - Решить на железную болванку массой 100кг падает с высоты 4м паровой молот массой...
2 - Іть. як оформляти читацький щоденник учня 8 класу?...
2 - Краткое содержание и главные герои произведения а.п.чехова человек в футляре...
3 - Периметр прямоугольника равен 24 см сторона равна 7 смчему равна площадь прямоугольника?...
1 - Очём рассказ волшебник изумрудного города...
3 - Что можно понять прочитав рассказ человек на часах?...
2
Сначала рассмотрим первую сетку (сетку А) на рисунке. Сопротивления проволочных элементов этой сетки обозначим как R1, R2 и R3.
1. Для начала определим эквивалентное сопротивление двух параллельно соединенных проволочных элементов R1 и R2. По правилу параллельного соединения сопротивлений, их эквивалентное сопротивление (R12) будет равно:
1/R12 = 1/R1 + 1/R2
Умножим обе части уравнения на R1R2:
R2 + R1 = R12R2 + R12R1
R2 + R1 = R12(R1 + R2)
R2 + R1 = R12(R1 + R2)
R1 + R2 = R12(R1 + R2)
Теперь определим эквивалентное сопротивление R12 всей параллельно соединенной ветви, включая третий проволочный элемент R3. Для этого мы рассматриваем R12 и R3 как два сопротивления, соединенные последовательно:
R12R3/(R12 + R3)
Теперь у нас есть эквивалентное сопротивление всей сетки A, обозначено как RA:
RA = R12R3/(R12 + R3)
Аналогично можно провести анализ для сетки B. Эквивалентное сопротивление всей сетки B, обозначено как RB, будет равно:
RB = R17R11/(R17 + R11)
Информация о сопротивлениях R1, R2, R3, R11 и R17 не предоставлена в вопросе. Если у вас есть значения этих сопротивлений, вы можете подставить их в уравнения, чтобы найти эквивалентные сопротивления сеток A и B.
Важно отметить, что результаты будут зависеть от конкретных значений сопротивлений R1, R2, R3, R11 и R17, поэтому без этих значений мы не можем дать более конкретного ответа.