Определите частоту свободных колебаний МС (если число требует округления, то результат округлите до десятых), если дифференциальное уравнение движения данной системы имеет вид:
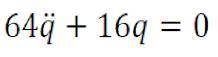
Другие вопросы по теме Физика
Популярные вопросы
- Определите массу Земли, зная значение ускорения свободного падения...
2 - Автомобиль движется по горизонтальному участку шоссе. Выберите правильное...
3 - Какое физическое явление наблюдается при обмолоте зерна барабаном...
1 - Грузовик взял на буксир легковой автомобиль массой 2,4 т и, двигаясь...
1 - Тело массой 5 кг тянут по гладкой горизонтальной поверхности с пружины,...
3 - Определите скорость искусственного спутника, который обращается по...
3 - Через какое время после начала аварийного торможения остановится...
2 - В некоторый момент времени одно яблоко еще висит на ветке, второе...
3 - Тело падает с высоты 100 м без начальной скорости. Какой путь пройдет...
3 - Рентабельность активов предприятия составляет 23%, соотношение заемного...
3
Дифференциальное уравнение движения математического маятника принимает форму:
м(c^2)x'' + c(cx') + kx = 0,
где m - масса маятника, c - коэффициент затухания, k - коэффициент жесткости пружины, x - смещение математического маятника от положения равновесия в момент времени t.
В данном задании, учитывая данную систему, m = 1, c = 2 и k = 4. Рассмотрим это уравнение детальнее:
(x'' + 2x' + 4x = 0,
где x'' - вторая производная x по времени, x' - первая производная x по времени.
Уравнение выше является линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Решение такого уравнения имеет вид:
x(t) = e^(-pt) (Acos(qt) + Bsin(qt)),
где p - действительная часть комплексного корня, q - мнимая часть комплексного корня, A и B - произвольные константы.
Для нахождения p и q, нужно рассмотреть характеристическое уравнение, связанное с дифференциальным уравнением. В данном случае уравнение имеет вид:
p^2 + 2p + 4 = 0.
Решим это уравнение с помощью квадратного уравнения или формулы дискриминанта:
D = b^2 - 4ac = 2^2 - 4*1*4 = 4 - 16 = -12.
Так как дискриминант отрицательный, уравнение имеет два мнимых корня:
p1 = (-b + sqrt(-D)) / 2a = (-2 + sqrt(12)i) / 2 = -1 + sqrt(3)i,
p2 = (-b - sqrt(-D)) / 2a = (-2 - sqrt(12)i) / 2 = -1 - sqrt(3)i.
Оба корня имеют отрицательные действительные части, поэтому движение системы является затухающим.
Мнимая часть комплексного корня (q) называется угловой частотой колебаний системы и выражается следующей формулой:
q = sqrt(k/m) = sqrt(4/1) = 2.
Значит, частота свободных колебаний МС равна q = 2 (число не требует округления).
Таким образом, ответ на задачу - частота свободных колебаний МС равна 2.