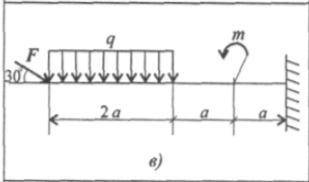
Определить величины реакций в заделке
F1=22 kH
q=3 kH/м
m=50kH*м
a=0.3 м

Для определения величин реакций в заделке, необходимо использовать принцип равновесия. Принцип равновесия говорит о том, что сумма всех сил, действующих на тело, должна быть равна нулю. В данном случае, силы действуют в горизонтальном и вертикальном направлениях.

Сначала рассмотрим силы в горизонтальном направлении. В заданной системе силы F1 и q являются горизонтальными силами. Сумма этих сил равна нулю, так как стержень находится в равновесии по горизонтали.

F1 + q*l + R1 = 0

где F1 - известная сила равная 22 кН (килоньтон), q - известная равная 3 кН/м (килоньтон на метр), l - известная длина равная 0.3 м (метр), R1 - искомая реакция в заделке.

Теперь рассмотрим силы в вертикальном направлении. В данном случае, сила тяжести (m*g) и вертикальная составляющая силы q, равна сумме величины реакции в заделке (R1) и реакции опоры (R2).

m*g + q*l*sin(θ) = R1 + R2

где m - известная масса равная 50 кН*м (килоньтон на метр), g - ускорение свободного падения примерно равное 9.8 м/с^2 (метр на секунду в квадрате), q - известная равная 3 кН/м (килоньтон на метр), l - известная длина равная 0.3 м (метр), θ - угол наклона.

Находим значение угла наклона (θ). Для этого необходимо рассмотреть треугольник, образованный стержнем и горизонтальной осью. Возьмем синус угла наклона.

sin(θ) = a/l
θ = arcsin(a/l)

где a - известная длина равная 0.3 метра (м), l - известная длина равная 0.3 метра (м).

Теперь можно подставлять значения в найденные уравнения:

F1 + q*l + R1 = 0
22 + 3*0.3 + R1 = 0
22 + 0.9 + R1 = 0
R1 = -22.9 кН (килоньтон)

m*g + q*l*sin(θ) = R1 + R2
50*9.8 + 3*0.3*sin(θ) = 22.9 + R2

Для нахождения значения R2, необходимо знать угол наклона (θ). Для этого рассмотрим треугольник, образованный стержнем и горизонтальной осью. Возьмем косинус угла наклона.

cos(θ) = a/l
θ = arccos(a/l)

После определения угла наклона (θ), можно подставить его значение во второе уравнение и решить его, чтобы найти значение R2.

Обратите внимание, что значения реакций в заделке (R1 и R2) получены в отрицательной форме, так как силы направлены в противоположную сторону.