Определить скорость, с которой движется тень луны по земной поверхности во время полного солнечного затмения, если оно налбюдается на экваторе. для простоты считать, что солнце, земля и луна находятся в одной плоскости, а земная ось к этой плоскости перпендикулярна. скорость света считать бесконечно большой по сравнению со всеми остальными скоростями. радиус луной орбиты r=3,8.10^5 км

Так как не сказано где мы считаем скорость тени, то я буду считать ее на экваторе. Будем работать в система отсчета, в которой Земля покоится.

За 1 секунды Солнце и Луна переместятся с востока на запад на расстояние  и . Поясняющий рисунок см в приложении. (наблюдаем в точке M1)

wc и wl-угловые скорости вращения Солнца и Луны вокруг центра Земли. Они нам кстати известны.

По сути MM1-это и есть скорость тени Луны.

Из подобиев трегольников видно, что искомая скорость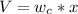 (если положим, что OA=Rc, ну так как расстояние до Луны очень мало по сравнению с расстоянием до Солнца.)

Нам нужно найти x, для этого опять же воспользуемся подобиями треугольников

(где r-радиус Земли)

км/с

- продолжительность месяца. -  продолжительность суток.