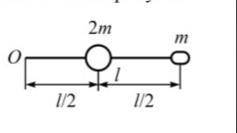
определить момент импульса. Физика. Два шара массами m и 2m (m = 10 г) закреплены на тонком невесомом стержне длиной l = 40 см так, как показано на рисунке. Определите момент импульса системы, вращающейся с частотой ν относительно оси, перпендикулярной стержню и проходящей через его конец. Размерами шаров пренебречь.

Для начала давайте определение понятия "момент импульса". Момент импульса твердого тела относительно определенной точки равен произведению момента инерции этого тела относительно этой точки на его угловую скорость.

В данной задаче у нас есть два шара, закрепленные на стержне. Давайте рассмотрим шар массой m и обозначим его расстояние от оси вращения (точка О на рисунке) как R1. Соответственно, у второго шара массой 2m расстояние от оси вращения обозначим как R2 (40 см).

Предположим, что система вращается с угловой скоростью ω, которую необходимо найти. Момент инерции шара можно выразить формулой I = mR^2, где m - масса шара, а R - его расстояние от оси вращения.

Теперь рассмотрим момент инерции первого шара: I1 = mR1^2.
Аналогично, момент инерции второго шара: I2 = (2m)(R2^2) = 4mR2^2.

Поскольку вращение происходит относительно оси, перпендикулярной стержню и проходящей через его конец, то система шаров выступает как два плавающих момента импульса.

Момент импульса первого шара: L1 = I1ω.
Момент импульса второго шара: L2 = I2ω.

Момент импульса системы: L = L1 + L2.

Теперь подставим значения и найдем момент импульса системы:
L = mR1^2ω + 4mR2^2ω.

Для удобства подставим значения R1 = R и R2 = 40 см = 0.4 м и m = 10 г = 0.01 кг.

L = (0.01 кг)(R^2)ω + 4(0.01 кг)(0.4 м)^2ω = 0.01(R^2)ω + 4(0.01)(0.4^2)ω = 0.01R^2ω + 0.064ω.

Теперь нам нужно найти угловую скорость ω, используя информацию о частоте вращения системы ν. Связь между частотой и угловой скоростью: ω = 2πν.

L = 0.01R^2ω + 0.064ω = 0.01R^2(2πν) + 0.064(2πν) = 0.02πR^2ν + 0.128πν.

Таким образом, мы определили момент импульса системы вращающихся шаров в зависимости от их расстояния от оси вращения R и частоты вращения ν.