1. Физика
  2. Определи модуль центростремительного

Определи модуль центростремительного ускорения тела, которое равномерно движется по окружности с радиусом 0,9 м. Период обращения равен 2 с. (ответ округли до сотых долей)

ghrtoung ghrtoung    1   11.10.2021 01:21    36

Ответы
mila336 mila336  11.10.2021 01:30

a=\frac{4*\pi^2}{4}*0,9=8,88 м/с².

Объяснение:

Дано:

R=0,9 м. - радиус окружности;

T=2 с. - период обращения тела;

Требуется найти модуль центростремительного ускорения a тела.

Одна из формул, по которой можно найти центростремительное ускорение имеет вид:

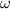a=\omega^2*R

Где \omega - угловая скорость, которую можно найти из формулы для периода обращения:

T=\frac{2*\pi}{\omega}

Откуда угловая скорость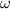 \omega равна:

\omega=\frac{2*\pi}{T}

Подставляя данное значение в формулу для центростремительного ускорения, получим:

a=(\frac{2*\pi}{T})^2*R=\frac{4*\pi^2}{T^2}*R

Число Пи примем за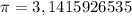 \pi=3,1415926535

Все значения известны, считаем:

a=\frac{4*\pi^2}{4}*0,9=8,88 м/с². - это и будет ответ.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Физика
Leafyllall Leafyllall  10.10.2019 14:07
Горизонтальний провідник масою 4г і завдовжки 15 см лежить на рейках у пертикальному магнітному полі індукиісю 30 мтл. визначте коефіцієнт тертя, якщо за сили струму в провіднику...
никиумняшка никиумняшка  10.10.2019 14:06
вас , 15 ​задние 5 установить соотвествие...
mrtopgame mrtopgame  10.10.2019 14:05
Ерс джерела струму становить 10 в . коли до нього приэднали опір величиною у 2 ом , то сила струму в колі стала рівною 4 а . визначте струм короткого замикання...
MARZHIVANKINA MARZHIVANKINA  10.10.2019 14:01
Визначити ерс індукції в котушці з 100 витків в якій за 10 мс магнітний потік змінюється на 3мвб...
умник1235678 умник1235678  10.10.2019 14:00
При замыкании источника тока на 5 ом напряжение на равно 10 в, а при замыкании на 12 ом напряжение равно 12 в. определить внутреннее сопротивление и эдс источника тока....
salgis salgis  10.10.2019 13:54
8. (4 ) прямолінійний провідник завдовжки 60 см розташований в однорідному магнітному полі індукцією 2,4 мтл під кутом 30° до ліній магнітної індукції поля. визначте: а) силу...
oborinamascha oborinamascha  10.10.2019 13:54
5. (46) в сосуд с водой, массой 5 кг при температуре 7°с, опустилиболванку массой 3 кг нагретую до 540°с. в результате температураводы установилась 40°с. какова удельная теплоёмкость...
FTA72артем FTA72артем  10.10.2019 13:53
Сколько тонн кизяка надо сжечь что бы полученное количество теплоты равнялось 9*10 кдж механической энергии?...
angelina0512200 angelina0512200  13.12.2021 13:25
физике. 1) Учитывая точечный заряд подвески -2,7 × 10 ^-⁶ в вакууме.Определите напряженность электрического поля этого заряда на расстоянии 1 см. Нарисуйте поле заряда и укажите...
Zangerange Zangerange  13.12.2021 13:27
Масса: 2кгМасса сосуда: 600грНайти: объем сосуда...

Популярные вопросы