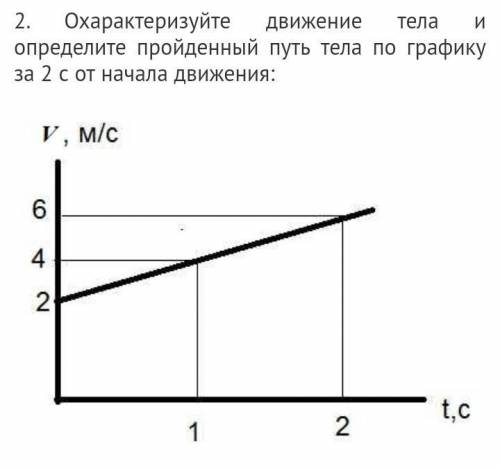
Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения: ЗА ПРАВИЛЬНЫЙ ОТВЕТ

Движение тела по графику можно охарактеризовать следующим образом:

1. Сначала тело находится в покое, так как график показывает горизонтальную прямую линию на протяжении первых 2 секунд. Поэтому скорость тела в начале движения равна нулю.

2. Затем график показывает, что тело начинает равномерно ускоряться вперед, так как прямая линия на графике становится все более крутой. Ускорение может быть вызвано действием силы, например, толчком или тягой.

3. Закончившееся ускорение указывает на то, что тело достигает своей максимальной скорости и движется равномерно прямолинейно. Как видно из графика, горизонтальная прямая линия обозначает это равномерное движение. Скорость тела остается постоянной.

Чтобы найти пройденный путь тела за указанное время (2 секунды), нам нужно вычислить площадь под графиком за это время. Это можно сделать, разбивая график на прямоугольники, треугольники и трапеции и находя их площадь.

В данном случае, чтобы решить задачу, можно разделить график на прямоугольник и треугольник. Сначала найдем площадь прямоугольника, и затем площадь треугольника.

1. Площадь прямоугольника:
Ширина прямоугольника равна времени, а высота равна скорости. Чтобы найти ширину прямоугольника, нужно взять разность конечного и начального времени: 2 с - 0 с = 2 с. Чтобы найти высоту прямоугольника, нужно взять значение скорости в тот момент времени, когда тело достигло своей максимальной скорости (после ускорения). Это значение скорости можно прочитать с графика и оно равно примерно 4 м/с.

Площадь прямоугольника равна ширине умноженной на высоту: 2 с * 4 м/с = 8 м.

2. Площадь треугольника:
Треугольник имеет базу, равную разности между конечным и начальным временем, т.е. 2 с - 0 с = 2 с. Высота треугольника равна скорости в начале движения, которая равна 0 м/с, так как тело было в покое.

Площадь треугольника равна половине произведения базы на высоту: (1/2) * 2 с * 0 м/с = 0 м.

Суммируем площади прямоугольника и треугольника: 8 м + 0 м = 8 м.

Таким образом, пройденный путь тела за 2 секунды от начала движения составляет 8 метров.