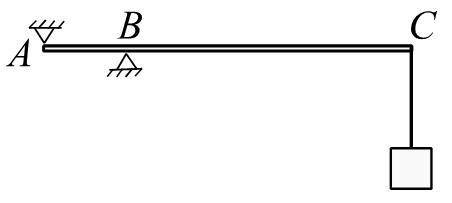
Oднородная горизонтально расположенная балка массой 60 кг и длиной 4 м шарнирно закреплена в точке А (см. рис.). Расстояние АВ равно 2 м. К точке С привязан груз массой 40 кг. Найти отношение силы реакции в опоре В к силе реакции в шарнире А.
Другие вопросы по теме Физика
Популярные вопросы
- 3 ксегашInau е ушиороиш ёшро -corperneyotpaceno olparyzaggrewned nag zugarespoenye...
3 - ОЧЕНЬ До десяти нужно сдать....
1 - Ядрышко это место образования 1)ДНК 2)хромосом 3)лизосом 4)рибосом...
2 - К одной языковой семье относятся: 1) Финны и литовцы 2) Армяне и башкиры 3) Татары...
1 - Cuando los humanos te llegaron a america que benian persigiendo...
1 - В чем на ваш взгляд выражается народный дух оперы Державина Рудокопы ? Насколько...
3 - Решите задачу с системы уравнений.найдите площадь прямоугольного триугольника,гипотенуза...
3 - В модельном доме Фирдовс сшили 30 новых моделей одежды в чеченской национальной...
2 - Написать 7 предложений о своей квартире только с глаголом have got...
1 - Для чего необходима утилизация электросберегающих элементов(батарейка)? Написать...
3
Для начала, обозначим силу реакции в опоре В как F_В и силу реакции в шарнире А как F_А. Используем предположение, что балка в равновесии.
Сумма моментов сил относительно точки А должна равняться нулю:
M_А = М_В + М_С = 0
Момент силы F_В относительно точки А равен: М_В = F_В * АВ * sin(α), где α - угол между F_В и АВ.
Момент силы F_С относительно точки А равен: М_С = F_С * АС * sin(β), где β - угол между F_С и АС.
Так как балка однородная и расположена горизонтально, то легко заметить, что углы α и β равны 90 градусам, поскольку F_В и F_С направлены перпендикулярно к АВ и АС соответственно.
С учетом этого, можем записать:
F_В * АВ * sin(90°) + F_С * АС * sin(90°) = 0
Учитывая, что sin(90°) = 1, получаем:
F_В * АВ + F_С * АС = 0
Далее, рассмотрим вертикальное равновесие системы. Сумма вертикальных компонент сил равна нулю:
ΣF_y = F_А * cos(γ) + F_В * cos(δ) - F_С - масса_балки * g - масса_груза * g = 0
где γ и δ - углы между F_А и вертикалью, F_В и вертикалью соответственно, g - ускорение свободного падения.
Учитывая, что cos(γ) = cos(δ) = 0 (поскольку F_А и F_В направлены по горизонтали), получаем:
F_С = масса_балки * g + масса_груза * g
Теперь можем подставить F_В и F_С в уравнение:
F_В * АВ + F_С * АС = 0
F_В * 2 + (масса_балки * g + масса_груза * g) * 4 = 0
А теперь найдем отношение силы реакции в опоре В к силе реакции в шарнире А:
F_В / F_А = (-масса_балки * g - масса_груза * g) * 4 / (-масса_балки * g)
F_В / F_А = (масса_груза + масса_балки) * 4 / масса_балки
Таким образом, отношение силы реакции в опоре В к силе реакции в шарнире А равно:
(масса_груза + масса_балки) * 4 / масса_балки