Нужна с по какой радиус r должен иметь алюминиевый шарик,натертый парафином, чтобы он "плавал" в воде, погрузившись ровно наполовину?

Дано:

кг/м³ — плотность алюминия

кг/м³ — плотность воды

Н/м — поверхностное натяжение воды

м/с² — ускорение свободного падения

============================

Найти: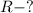 — радиус шара

============================

Решение. Парафин не смачивается водой. На шар действуют три силы: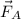 — сила Архимеда; 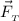— сила тяжести; 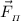— сила поверхностного натяжения воды.

Условие равновесия:

Распишем силы до тех величин, которые известны и надо найти:

(тут так как в жидкости находится только половина шара)

============================

ответ: 2,23 мм.

Сила поверхностного натяжения направлена перпендикулярно поверхности воды - для нашего случая к центру шарика.

Лаплассово давление P=2σ/r , где σ= 73 * 10^-3 Н/м - коэффициент поверхностного натяжения.

Для слоя воды расположенного под углом α к вертикали -

Площадь слоя

dS = 2*π*r*r*sin (α)*dα

Сила

dF = P dS = 2σ/r * 2*π*r*r*sin (α)*dα = 4* π* σ* r* sin (α)*dα

Нас интересует проекция этой силы на вертикальную ось

dFy= dF*cos(α) = 4* π* σ* r* sin (α)* cos(α) *dα = 2*π* σ* r* sin(2α) *dα

Интегрируем эти слои от 0 до π/2

F = ∫ dFy = ∫ π* σ* r* sin(2α) *d(2α) =  2*π*r*σ  - это сила поверхностного натяжения для шарика наполовину в воде.

Объем шарика

V = 4/3 π*r^3

Масса

m = 4/3 π*r^3 ρ(ал)

Сила Тяжести

Fт = mg = 4/3 π*r^3 ρ(ал) * g

Архимедова сила

F а = 2/3 π*r^3 ρ(в) * g  - шар наполовину в воде

Fa + F = Fт

Откуда

2/3 π*r^3 ρ(в) * g  + 2*π*r*σ   = 4/3 π*r^3 ρ(ал) * g

( 2ρ(ал)-ρ(в) ) r^2 * g = 3σ

r = √ (3σ/(g*(2ρ(aл) - ρ(в

Подставляя значения ρ(aл) = 2700 кг/м^3  ρ(в)= 1000 кг/ м^3

Получаем

r ~= 0.0023 м = 2.3 мм