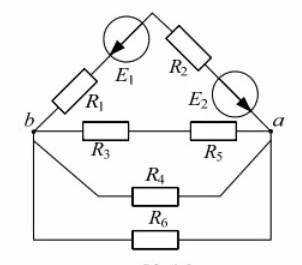
Нужна , найти по методу узловых потенциалов, + закон киргофа

Чтобы решить эту задачу с использованием метода узловых потенциалов и закона Кирхгофа, нам необходимо выполнить следующие шаги:

1. Найдем узловые потенциалы в каждой точке схемы. Узловой потенциал обозначается буквой V и измеряется в вольтах.
- Выбираем один из узлов в схеме и присваиваем ему значение потенциала V = 0V. Это будет наша опорная точка.
- Обозначим потенциалы остальных узлов как V1, V2 и V3.

2. Напишем уравнение для каждого узла, используя закон Кирхгофа для тока.
- В узле 1: I1 = I2 + I3
- В узле 2: I2 - I3 = I4
- В узле 3: I1 - I4 = I5

3. В уравнениях заменим токи через разность потенциалов и сопротивления:
- В узле 1: (V1 - V)/(R1+R2) = (V2 - V1)/R1 + (V3 - V1)/R2
- В узле 2: (V2 - V1)/R1 - (V3 - V2)/R2 = (V3 - V2)/R3
- В узле 3: (V1 - V3)/(R1+R3) - (V3 - V2)/R2 = (V3 - V4)/R4

4. Раскроем скобки и приведем уравнения к более простому виду:
- В узле 1: (V1 - V)/(R1+R2) = V2/R1 + V3/R2 - V1/R1 - V1/R2
- В узле 2: V2/R1 - V3/R2 + V3/R3 = V3/R2
- В узле 3: V1/(R1+R3) - V3/(R1+R3) - V3/R2 = V3/R4 - V4/R4

5. Перенесем все члены с V на одну сторону, чтобы уравнения имели вид Ax = B, где A и B - известные коэффициенты, а x - неизвестные потенциалы.
- В узле 1: -V1/R1 - V1/R2 + V2/R1 + V3/R2 = V/R1 + V/R2
- В узле 2: -V2/R1 + V3/R2 + V3/R3 = -V3/R2
- В узле 3: V1/(R1+R3) - V3/(R1+R3) + V3/R2 - V3/R4 + V4/R4 = 0

6. Запишем уравнения для всех узлов в матричной форме: AX = B, где X - вектор неизвестных потенциалов, A - матрица коэффициентов, B - вектор известных членов.
| (-1/R1 - 1/R2) 1/R1 1/R2 0 | | V1 | | V/R1 + V/R2 |
| (-1/R1) 1/R2 1/R3 -1/R2 | | V2 | | -V3/R2 |
| (1/(R1+R3)) -1/(R1+R3) 1/R2 -1/R4 | | V3 | = | 0 |
| 0 0 0 1/R4 | | V4 | | 0 |

7. Решим полученную систему уравнений методом Гаусса или другим способом решения системы линейных уравнений.

8. Подставим найденные значения потенциалов обратно в уравнения, чтобы найти значения токов или других неизвестных величин.

Таким образом, мы сможем найти значения потенциалов в каждой точке схемы с использованием метода узловых потенциалов и закона Кирхгофа.