Нудна , модуль вектора перемещения 10км, определите проекции вектора на оси координат, как на рисунке 20,а,б.
Другие вопросы по теме Физика
Популярные вопросы
- Я устраиваю супер акцию! ответь первым на супер лёгкий во и получи...
1 - АВ диаметр окружности с центром О . найдите угол DCO если ОА=ОС=АС...
3 - Назовите художественно-выразительное средство, используемое в следующих...
3 - Оберіть розподільну властивість множення будь ласка)))(a + b)c =...
1 - Две перпендикулярные прямые прямые которые совпадают, называю ,...
2 - NaCl=HCl=CuCl2=CuO=Cu(OH)2=CuSO4 напишіть використовуючи формули,...
3 - Запишите текст, вставляя глаголы из скобок: в части один в форме...
2 - Найдите 45% от 75, в ответе запишите десятичную дробь. ...
2 - Мәтін стилін ,түрін анықтаңыз...
2 - Решите вроде там не сложно, но я не могу) Заранее...
3
а) Дано:
========================
Найти: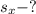
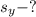
========================
Решение. Определим формулы нахождения проекций перемещения на оси OX и OY:
Определим значения искомых величин:
ответ: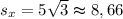 км;
км; 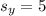 км.
км.
б) Дано:
========================
Найти: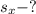
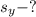
========================
Решение. Определим формулы нахождения проекций перемещения на оси OX и OY:
Определим значения искомых величин:
ответ: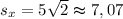 км;
км;  км.
км.