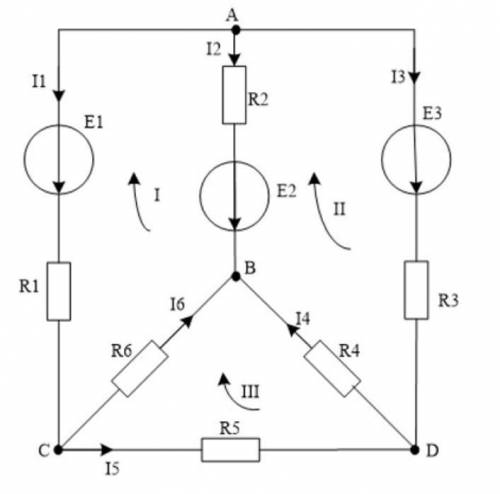
Необхідно скласти рівняння за першим законом Кірхгофа для наступного ланцюга:

Для решения данной задачи, мы будем использовать первый закон Кирхгофа, также известный как закон сохранения заряда.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов на любом узле в цепи равна нулю. То есть, если мы возьмем узел и нарисуем входящие и исходящие ветви, сумма входящих токов должна быть равна сумме исходящих токов.

Давайте назовем начальную точку нашего цепи узлом A и конечную точку - узлом B. Тогда на узле A должны суммироваться все входящие и исходящие токи в точке A. Также на узле B должны суммироваться все входящие и исходящие токи в точке B.

Давайте обозначим неизвестные токи в цепи следующим образом:
- i1: ток, протекающий через первый резистор,
- i2: ток, протекающий через второй резистор,
- i3: ток, протекающий через третий резистор.

Теперь рассмотрим узел A. Входит ток i1 из источника тока и ток i3 через третий резистор. Таким образом, сумма входящих токов равна i1 + i3. Итак, мы можем написать первое уравнение:

i1 + i3 = ...

Теперь рассмотрим узел B. В него входит ток i2 из второго резистора. Таким образом, сумма входящих токов равна i2. Итак, мы можем написать второе уравнение:

i2 = ...

Теперь обратимся к узлу A снова. Из данного узла исходит ток i1 в первый резистор и ток i2 во второй резистор. То есть, сумма исходящих токов равна i1 + i2. Итак, мы можем написать третье уравнение:

... = i1 + i2

Теперь у нас есть система из трех уравнений с тремя неизвестными токами i1, i2 и i3. Мы можем решить эту систему используя методы алгебры.