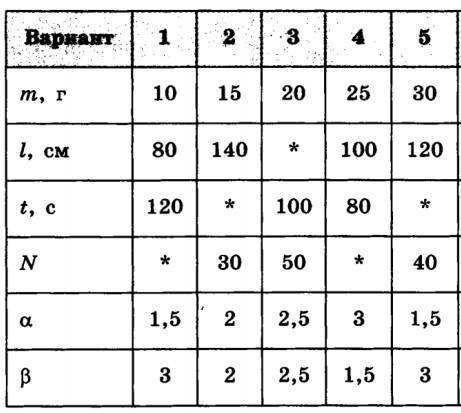
Небольшой грузик массой m подвешен на легкой нерастяжимой нити длиной l. При малом отклонении грузика от равновесия он колеблется в вертикальной плоскости и за время t совершает N колебаний. Определите значение величины, обозначенной *. Во сколько раз изменится период колебаний такого маятника при увеличении длины нити в α раз? Во сколько раз изменится период колебаний при увеличении массы грузика в β раз? 5 вариант

Объяснение:

Так как по условию грузик небольшой, то его размерами можно пренебречь и считать его материальной точкой.  Так как по условию нить - лёгкая и нерастяжимая, то её массой и упругими силами можно пренебречь. Тогда колеблющийся грузик можно считать математическим маятником.  Период колебаний такого маятника T=2*π*√(l/g), где l - длина нити, g - ускорение свободного падения. Так как период не зависит от массы грузика, то при увеличении его массы в β раз период не изменится. Если длину нити увеличить в α раз, то её длина станет равной l1=l*α, и тогда период колебаний станет равным T1=2*√(l1/g)=2*π*√(l*α/g). Отсюда T1/T=√α, т.е. период колебаний увеличится в √α раз.  Если известно время t N колебаний, то N=t/T=(t*√g)/(2*π*√l). Если известно число колебаний N, то время t=T*N=2*π*N*√(l/g). Если известны N и t, то l=t²*g/(4*π²*N²).

Для решения этой задачи, нам понадобится изучить законы колебаний простого математического маятника.

1. Период колебаний математического маятника определяется формулой:

T = 2π * √(l/g)

где T - период колебаний, l - длина нити, g - ускорение свободного падения.

2. Зная период колебаний, можно определить частоту колебаний, которая выражается формулой:

f = 1/T

где f - частота колебаний.

Теперь, перейдем к решению задачи.

1. Определим первоначальное значение периода колебаний:

T1 = t/N

где T1 - первоначальное значение периода колебаний, t - время, N - количество колебаний.

2. Увеличим длину нити в α раз:

l2 = α * l

3. Рассчитаем новое значение периода колебаний:

T2 = 2π * √(l2/g)

4. Определим изменение периода колебаний:

ΔTl = T2 - T1

5. Выразим изменение периода колебаний в процентах:

ΔTl% = (ΔTl/T1) * 100%

Теперь рассмотрим вторую часть задачи.

1. Увеличим массу грузика в β раз:

m2 = β * m

2. Рассчитаем новое значение периода колебаний:

T3 = 2π * √(l/g)

3. Определим изменение периода колебаний:

ΔTm = T3 - T1

4. Выразим изменение периода колебаний в процентах:

ΔTm% = (ΔTm/T1) * 100%

Таким образом, чтобы ответить на поставленный вопрос, нужно рассчитать значения ΔTl%, ΔTm%, а затем сравнить их. Ответом будет то, во сколько раз ΔTl% отличается от ΔTm%.