Небольшой брусок лежит на краю деревянной доски длиной 1 = 1 м. Если доску (наклонить так, что угол с горизонтом составит а, то брусок начнёт соскальзывать (при
меньшем наклоне он соскальзывать не будет). При этом, если доску отполировать так,
что коэффициент трения уменьшится вдвое, то при том же угле наклона брусок достиг-
нет нижнего края доски за t = 894 мс. Найдите угол а.(1сек=1000мс)ответ 30 градусов решите максимально подробно
Другие вопросы по теме Физика
Популярные вопросы
- Определите по координатам место.8* северной широты и 80* восточной долготы....
3 - Когда гремел мазурки гром, в огромной зале все дрожало, паркет трещал под каблуком,...
1 - Какие проблемы были в сельском хозяйстве империи? 20 века...
1 - Сочинение, эссэ. роль знаков препинания в тексте?...
3 - Перевели тё в арабские цифры cdlxxi ccclxxix...
3 - Найти значение выражения 0,5подкорень256...
2 - Поезд км в 4 часа сколько времени потребуется чтобы пройти 630км если он будет...
2 - 3целых две пятых минус 3 целых одна шестая =...
2 - Туристы ехали на автобусе 4 ч со скоростью 70 км/ч и шли пешком 6 ч со скоростью...
3 - Пожплуйста нужно диалог по как я провел летние каникулы? нужно...
1
30°
Объяснение:1. Составим 2-ой закон Ньтона для второй ситуации (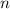 ),
),
Здесь уже учтено, что:
Из первого уравнения, следует:
Из этого уравнения видно, что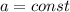
Тогда можно записать уравнение кинематики для равноускоренного движения:
2. Теперь составим уравнение при коэффициенте трения равным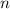
Т. к в условии сказано, что при углах меньше чем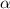 , брусок не скользит, а следовательно покоится, тогда можно взять угол немного меньший чем угол
, брусок не скользит, а следовательно покоится, тогда можно взять угол немного меньший чем угол 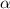 , т. е α ≈ β, и записать первое положение статики в момент
, т. е α ≈ β, и записать первое положение статики в момент 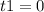
То есть тело только - только будеть скользить, поэтому можно рассмотреть предельный случай:
Подставляем коэффициент трения скольжения в закон равноускоренного движения: