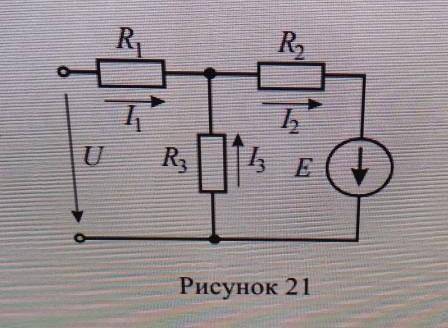
Найти токи в ветвях, если U=30 В, R1=R2=R3=20 Ом, E=60 В.

Добрый день! Рад быть вашим учителем и помочь вам с решением этой задачи.

На данной схеме мы имеем электрическую цепь, состоящую из источника ЭДС E, трех одинаковых сопротивлений R1, R2 и R3, и резистора R. На эту схему подается напряжение U.

Для решения данной задачи, мы можем применить закон Ома, который гласит, что ток в цепи (I) равен отношению напряжения (U) к сопротивлению (R).

В данной цепи у нас есть два источника электродвижущей силы (ЭДС) - E и U. Чтобы найти токи в ветвях, нам нужно вычислить суммарное сопротивление цепи (R_всего), используя формулу параллельного соединения резисторов, и затем применить закон Ома.

Для начала, найдем сопротивление всей цепи (R_всего). Так как резисторы R1, R2 и R3 соединены параллельно, их общее сопротивление можно вычислить по формуле:
1/R_всего = 1/R1 + 1/R2 + 1/R3.

Подставив значения R1 = R2 = R3 = 20 Ом, получим:
1/R_всего = 1/20 + 1/20 + 1/20 = 3/20.

Чтобы найти R_всего, возьмем обратное значение и получим:
R_всего = 20/3 Ом.

Теперь, используя закон Ома, можем найти ток в цепи (I):
I = U / R_всего.

Подставим значение U = 30 В и R_всего = 20/3 Ом и получим:
I = 30 / (20/3) = 30 * (3/20) = 4.5 А.

Таким образом, ток в цепи (I) равен 4.5 А.

Далее, для нахождения токов в ветвях, мы можем использовать закон Кирхгофа об узлах. Закон Кирхгофа гласит, что сумма входящих и исходящих токов в узле равна нулю.

На нашей схеме мы имеем два узла: узел A и узел B. Найдем токи в ветвях, начиная с узла A.

В узле A, сумма входящих и исходящих токов равна нулю:

I - I_1 - I_2 = 0,

где I_1 - ток, протекающий через резистор R1,
I_2 - ток, протекающий через резистор R2.

Теперь, использовав результаты предыдущих расчетов, можем выразить I_1 и I_2 через I:

I_1 = I * (R_всего / R1),
I_2 = I * (R_всего / R2).

Подставим значения и получим:
I - I * (R_всего / R1) - I * (R_всего / R2) = 0.

Упростим это уравнение:
I - (I * R_всего / R1) - (I * R_всего / R2) = 0,
I (1 - R_всего / R1 - R_всего / R2) = 0.

Теперь найдем I_1 и I_2, подставив значения:
I_1 = I * (R_всего / R1) = 4.5 * (20/3) / 20 = 3 А,
I_2 = I * (R_всего / R2) = 4.5 * (20/3) / 20 = 3 А.

Таким образом, токи в ветвях I_1 и I_2 равны 3 А.

Наконец, найдем ток I_3 через резистор R3. Так как резисторы R1, R2 и R3 соединены параллельно, ток I_3 также равен 3 А.

Итак, токи в ветвях:
I_1 = 3 А,
I_2 = 3 А,
I_3 = 3 А.

Надеюсь, я смог подробно объяснить вам решение этой задачи. Если у вас остались вопросы, пожалуйста, задавайте их.