Начертить ход лучей, изображенных на рисунке

В этой задаче нам закон Снеллиуса (закон преломления света). Угол падения света на поверхность связан с углом преломления соотношением:

, где:

— показатель преломления среды, из которой свет падает на границу раздела;

sinα — угол падения света — угол между падающим на поверхность лучом и нормалью (перпендикуляром) к поверхности;

— показатель преломления среды, в которую свет попадает, пройдя границу раздела;

sinβ— угол преломления света — угол между через поверхность лучом и нормалью к поверхности.

Чтобы начертить дальнейший ход луча, нужно узнать sinβ. Выразим sinβ:

= . В данной задаче n1 = 1 (для воздуха), n2 = 1,333 (для воды).

Вычислим дальнейший ход луча сначала для угла падения 60°:

sinβ =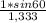 = = 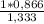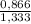≈ 0,6496624

Данному синусу соответствует угол в 40°. Теперь с транспортира строим угол преломления в 40°

Теперь вычислим дальнейший ход луча для угла падения в 30°:

= = ≈ 0,375

Данному синусу соответствует угол в 22°. Опять же с транспортира строим угол преломления.