Начальная скорость - 72км/ч
конечная скорость - 180 км/ч
найти скорость на половине пути

137 км/ч

Объяснение:

v1=72 км/ч    v2=180 км/ч   vx=?

===

s=(v2²-v1²)/(2*a)

s/2=(vx²-v1²)/(2*a)

Разделим левые и правые части уравнений

2=(v2²-v1²)/(vx²-v1²)

vx=√((v2²-v1²)/2 + v1²)=√((180²-72²)/2 + 72²)=137 км/ч

Пусть v0 = 72 км /ч , v2 = 180 .Тогда пусть пройденный за то время ,за которое произошло изменение скорости равно S1= (v2 ^2 - v0 ^2)/2a.Тогда половина пройденного пути равна S2 =  S1/2 = (v2 ^2 - v0 ^2)/4a.Запишем уравнение движение S2 = (v2 ^2 - v0 ^2)/4a = v0t + (at^2)/2 . Решим это уравнение относительно t  =  (-v0 +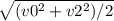 )/a .Тогда скорость на половине пути равна vx =v0 + at  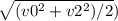= = 137 км /ч

ответ : 137 км/ч